
题目列表(包括答案和解析)
4、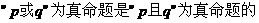 条件
条件
A.充分非必要条件 B.必要非充分条件
C.既非充分也非必要条件 D.充要条件
3、函数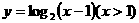 的反函数是(
)
的反函数是(
)
A.
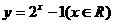 B.
B.
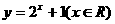
C.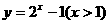 D.
D. 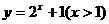
2、等差数列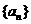 中,若
中,若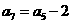 ,则
,则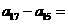 ( )
( )
A.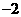 B.
B.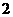 C.
C.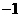 D.
D.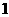
1、已知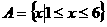 ,
,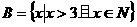 ,则
,则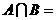 (
)
(
)
A.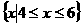 B.
B.
C. 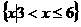 D.
D.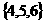
15  (12分)已知函数f (x)=
(12分)已知函数f (x)=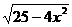 (
(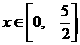 ),求出它的反函数
),求出它的反函数

16  (12分)设函数
(12分)设函数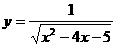 的定义域为A,B=
的定义域为A,B=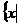
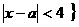 ,且A
,且A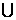 B=R,求实数
B=R,求实数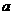 的取值范围
的取值范围 
17.(14分)已知函数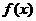 是偶函数,而且在
是偶函数,而且在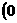 ,
,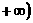 是减函数
是减函数 
⑴ 判断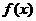 在
在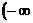 ,
,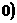 上是增函数还是减函数,并证明你的判断
上是增函数还是减函数,并证明你的判断 
⑵ 写出符合上述条件的一个函数 
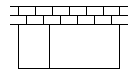
18  (14分)以墙为一边,用篱笆围成长方形的场地,并用平行于一边的篱笆隔开(如图)
(14分)以墙为一边,用篱笆围成长方形的场地,并用平行于一边的篱笆隔开(如图)  已知篱笆的总长为定值L,这块场地的长和宽各为多少时场地的面积最大?最大面积是多少?
已知篱笆的总长为定值L,这块场地的长和宽各为多少时场地的面积最大?最大面积是多少?
19  (14分)已知f (x)=log
a
(14分)已知f (x)=log
a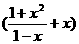 (a>0,a≠1).
(a>0,a≠1).
(Ⅰ)求f (x)的定义域;
(Ⅱ)判断f (x)的奇偶性并予以证明;
20  (14分)设
(14分)设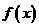 为定义在
为定义在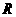 上的偶函数,当
上的偶函数,当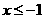 时,
时,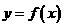 的图象是经过点
的图象是经过点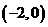 ,斜率为1的射线,又在
,斜率为1的射线,又在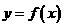 的图象中有一部分是顶点在
的图象中有一部分是顶点在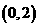 ,且过点
,且过点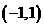 的一段抛物线
的一段抛物线  试求函数
试求函数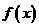 的表达式,并作出其图象.
的表达式,并作出其图象.
1  设集合P={1,2,3,4},Q={
设集合P={1,2,3,4},Q={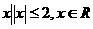 },则P∩Q等于
},则P∩Q等于
A.{1,2}
B  {3,4}
C
{3,4}
C  {1} D
{1} D  {-2,-1,0,1,2}
{-2,-1,0,1,2}
2  设函数f ( x )=2x+3,g (x+2)=f ( x ),则g ( x )的表达式是
设函数f ( x )=2x+3,g (x+2)=f ( x ),则g ( x )的表达式是
A.2x+1 B  2x-1 C
2x-1 C  2x-3 D
2x-3 D
 2x+7
2x+7
3  函数
函数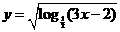 的定义域是:
的定义域是:
A.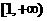 B.
B.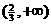 C.
C.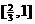 D.
D.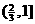
4  设0<a<1,实数x,y满足x+
设0<a<1,实数x,y满足x+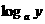 =0,则y关于x的函数的图象大致形状是 A
=0,则y关于x的函数的图象大致形状是 A
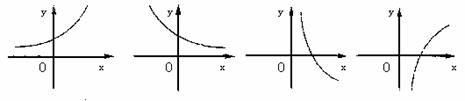 A
B
C
D
A
B
C
D
5  函数
函数 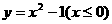 反函数是
反函数是
A 
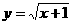
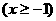 B
B 
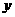 = -
= -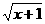
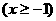
C 
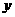 =
=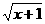
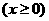 D
D 
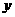 =-
=-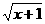
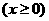
6  命题“方程
命题“方程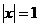 的解集是
的解集是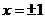 ”中,使用逻辑连结词的情况是
”中,使用逻辑连结词的情况是
A  没有使用逻辑连结词 B
没有使用逻辑连结词 B  使用了逻辑连结词“或”
使用了逻辑连结词“或”
C
 使用了逻辑连结词“且” D
使用了逻辑连结词“且” D  使用了逻辑连结词“非”
使用了逻辑连结词“非”
7  与函数y=x有相同图象的一个函数是
与函数y=x有相同图象的一个函数是

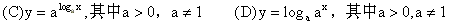
8  函数
函数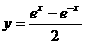 的反函数
的反函数
A  是奇函数,它在(0,+∞)上是减函数
是奇函数,它在(0,+∞)上是减函数  B
B  是偶函数,它在(0,+∞)上是减函数
是偶函数,它在(0,+∞)上是减函数 
C  是奇函数,它在(0,+∞)上是增函数
是奇函数,它在(0,+∞)上是增函数  D
D  是偶函数,它在(0,+∞)上是增函数
是偶函数,它在(0,+∞)上是增函数 
 9
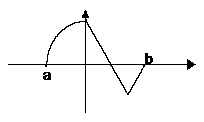
9  已知y=
已知y=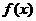 (
(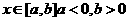 )的图象如右图所示,则y=
)的图象如右图所示,则y=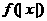 的图象为
的图象为
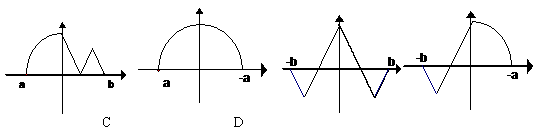 |
|||||
|
|
10  函数
函数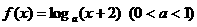 的图象必不过
的图象必不过
A  第一象限 B
第一象限 B  第二象限 C
第二象限 C  第三象限 D
第三象限 D  第四象限
第四象限
二  填空题(每题5分,共4题,满分20分)
填空题(每题5分,共4题,满分20分)
11  奇函数
奇函数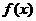 定义域是
定义域是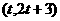 ,则
,则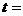

12  函数
函数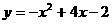 在区间[0,3]上的最大值是
在区间[0,3]上的最大值是  最小值
最小值  是
是 
13  设函数f (x)的反函数是f -1(x)=
设函数f (x)的反函数是f -1(x)=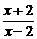 ,则f (4)=
,则f (4)=

14  函数
函数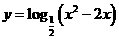 的单调递减区间是
的单调递减区间是

20.(14分) 已知函数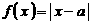 ,
,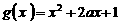 (
(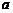 为正常数),且函数
为正常数),且函数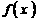 与
与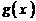 的图象在
的图象在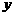 轴上的截距相等。(1)求
轴上的截距相等。(1)求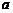 的值;(2)求函数
的值;(2)求函数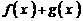 的单调递增区间;(3)若
的单调递增区间;(3)若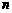 为正整数,证明:
为正整数,证明: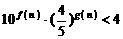 .
.
19.(14分)设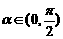 ,函数
,函数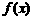 的定义域为
的定义域为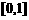 ,且
,且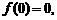
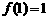 ,当
,当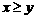 时,
时,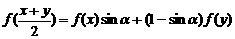 ,求:
,求:
(1) 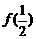 及
及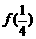 的值; (2)函数
的值; (2)函数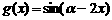 的单调递增区间;
的单调递增区间;
(3) 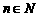 时,
时,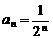 ,求
,求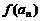 ,并猜测
,并猜测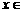
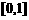 时,
时,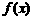 的表达式.
的表达式.
18.(14分)某地区预计明年从年初开始的前x个月内,对某种商品的需求总量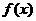 (万件)与月份x的近似关系为:
(万件)与月份x的近似关系为: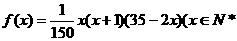 ,且
,且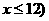 .
.
(1)写出明年第x个月的需求量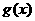 (万件)与月x的函数关系,并求出哪个月份的需求量最大,最大需求量是多少?
(万件)与月x的函数关系,并求出哪个月份的需求量最大,最大需求量是多少?
(2)如果将该商品每月都投放市场p万件(销售未完的商品都可以在以后各月销售),要保证每月都足量供应,问:p至少为多少万件?
17.(14分)已知数列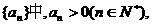 其前n项和为Sn,且S1=2,当
其前n项和为Sn,且S1=2,当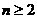 时,Sn=2an. (1)求数列
时,Sn=2an. (1)求数列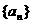 的通项公式; (2)若
的通项公式; (2)若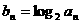 ,求数列
,求数列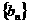 的前n项和.
的前n项和.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com