
题目列表(包括答案和解析)
2、过点A(1,2)且在两坐标轴上的截距的绝对值相等的直线共有( )条
A、1 B、2 C、3 D、4
1、 已知集合
已知集合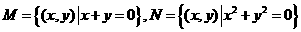 ,则有( )
,则有( )
A、M∪N=M B、M∪N=N C、M∩N=M D、M∩N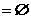
17. (本题满分12分)
已知集合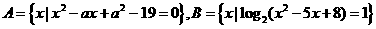 ,
,
集合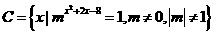 满足
满足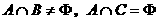 ,求实数
,求实数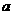 的值
的值
18 (本题满分12分)设函数
(本题满分12分)设函数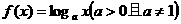 ,函数
,函数
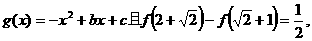
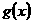 的图像过点A(
的图像过点A(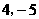 )及B(
)及B(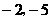 ),
),
(1)求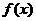 和
和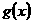 的表达式;
的表达式;
(2)求函数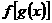 的定义域和值域
的定义域和值域
19 (本题满分12分)某种汽车购买时费用为10万元,每年应交保险费
(本题满分12分)某种汽车购买时费用为10万元,每年应交保险费 养路费及汽油合计为9千元,汽车维修费平均为:第一年2千元,第二年4千元,第三年6千元,…依次成等差数列逐年递增.问:这种汽车使用多少年报废最合算(即使用多少年的平均费用最少)?
养路费及汽油合计为9千元,汽车维修费平均为:第一年2千元,第二年4千元,第三年6千元,…依次成等差数列逐年递增.问:这种汽车使用多少年报废最合算(即使用多少年的平均费用最少)?
20 (本题满分12分)已知函数
(本题满分12分)已知函数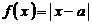 ,
,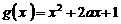 (
(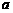 为正常数),且函数
为正常数),且函数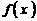 与
与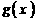 的图象在
的图象在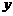 轴上的截距相等
轴上的截距相等 ⑴求
⑴求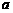 的值;
的值;
⑵求函数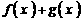 的单调递增区间
的单调递增区间
21 (文科学生做(本题满分12分)已知函数
(文科学生做(本题满分12分)已知函数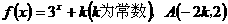 是函数
是函数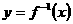 图像上的点
图像上的点 (Ⅰ)求实数
(Ⅰ)求实数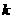 的值及函数
的值及函数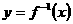 的表达式
的表达式
(Ⅱ)将函数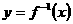 的图像沿
的图像沿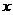 轴向右平移3个单位,得到函数
轴向右平移3个单位,得到函数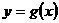 的图像
的图像 求函数
求函数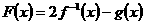 的最小值
的最小值
*21 (理科学生做)(本题满分12分)设函数
(理科学生做)(本题满分12分)设函数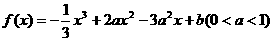
(1)求函数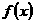 的极大值和极小值;
的极大值和极小值;
(2)当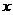 ∈[
∈[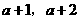 ]时,不等式
]时,不等式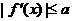 恒成立,求实数
恒成立,求实数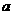 的取值范围.
的取值范围.
22 (文科学生做) (本小题满分14)已知函数
(文科学生做) (本小题满分14)已知函数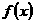 的定义域为
的定义域为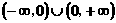 ,且满足条件:①
,且满足条件:①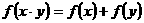 ,②
,②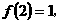 ③当
③当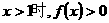
⑴求证:函数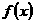 为偶函数;
为偶函数;
⑵讨论函数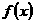 的单调性;
的单调性;
⑶求不等式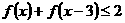 的解集
的解集
*22 (理科学生做) (本小题满分14)设函数
(理科学生做) (本小题满分14)设函数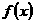 的定义域是R,对于任意实数
的定义域是R,对于任意实数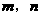 ,恒有
,恒有
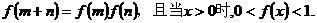
(1)求证: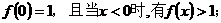
(2)判断函数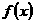 在R上的单调性;
在R上的单调性;
(3)设集合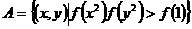 ,集合
,集合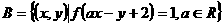 ,若
,若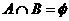 ,求实数
,求实数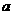 的取值范围
的取值范围
22. (本小题满分14分)
椭圆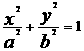 (a > b>0)的两个焦点为F1 (-c,0)、F2(c,0),M是椭圆上一点,满足
(a > b>0)的两个焦点为F1 (-c,0)、F2(c,0),M是椭圆上一点,满足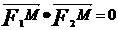 ;(I)求离心率e的取值范围
;(I)求离心率e的取值范围
(Ⅱ)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为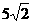
(1)求此时椭圆G的方程;
(2)设斜率为k (k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为A、B的中点,问:A、B两点能否关于过点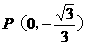 、Q的直线对称? 若能,求出^的取值范围;若不能,请说明理由
、Q的直线对称? 若能,求出^的取值范围;若不能,请说明理由
的文字说明、推理过程或计算步骤)。
17.(本小题满分12分)
已知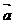 =(cos2a,slna);
=(cos2a,slna);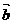 = (1,2sina-1),a∈(
= (1,2sina-1),a∈(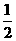 , π),
, π),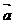 ·
·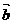 =
=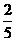 ,求cos(a+
,求cos(a+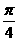 )是值
)是值
18(本小题满分12分)
已知p:f -1 (x )是,f (x )=1-3x的反函数,且| f -1 (a ) | <2
p:集合A = { x| x 2 +( a+2) x +l = 0,x∈R},B = { x | x >0},且A∩B=φ
求实数a的取值范围,使p、q中有且只有一个为真命题
 19(本小题满分12分)
19(本小题满分12分)
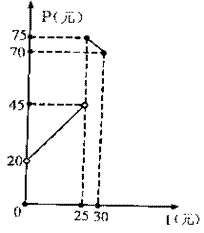
某种商品在30天内每件的销售价格P(元)与时问t(天)的函数关系用右图的两条线段表示:
该商品在30天内日销售量Q (件)与时问t (天)之间的关系如下表所示:
(I)根据提供的图像,写出该商品每件的销售价格P与时间t的函数关系式
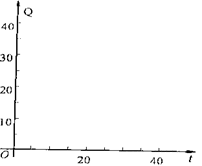 (Ⅱ)在所给直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数关系式
(Ⅱ)在所给直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数关系式
(Ⅲ)求该商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?(日销售金额一每件的销售价格×日销售量)
20(本小题满分12分)
如图,正三角形ABC的边长为2,D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠,使A、B、C三点重合,构成三棱锥A- DEF 。
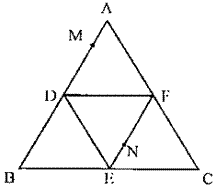 (I)求平面ADE与底面DEF所成二面角的余弦值
(I)求平面ADE与底面DEF所成二面角的余弦值
(Ⅱ)设点M、N分别在AD、EF上,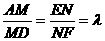 (λ>O,λ为变量)
(λ>O,λ为变量)
①当λ为何值时,MN为异面直线AD与EF的公垂线段?
请证明你的结论
②设异面直线MN与AE所成的角为a,异面直线MN与DF所成的角为β,试求a+β 的值
21(本小题满分12分)
已知函数,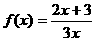 ,数列{an }满足
,数列{an }满足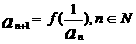
(I)求数列{an }的通项公式 (Ⅱ)记Tn =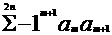
①求Tn ;②设数列{bn }的通项公式为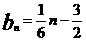 .求证:bn·Tn≤20
.求证:bn·Tn≤20
(符号“∑”表示将若干个数相加如,x1 + x2 +…+ xn 记作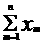 )
)
15. ; 16. ;
13. ; 14. ;
16.若二次函数f 1 (x ) 、 f 2(x ) 满足条件:f (x )= f 1 (x )+ f 2 (x )在(一∞,+∞)上单调递增,(2)g= f1 (x ) - f2 (x )对任意实数 x1 、x2 (x1 ≠x2)都有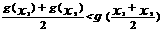 ,则f 1 (x ) =
,f 2 (x )= 。(只须填上你认为正确的一组即可)
,则f 1 (x ) =
,f 2 (x )= 。(只须填上你认为正确的一组即可)
高三数学期末综合练习(八)
班级 姓名 学号 得分
15.同学们都知道,在一次考试后,如果按顺序去掉一些高分,那么班级的平均分将降低;
反之,如果按顺序去掉一些低分,那么班级的平均分将提高. 这两个事实可以用数学语
言描述为:若有限数列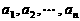 满足
满足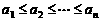 ,则
,则
(结论用数学式子表示).
14.若向量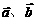 的夹角为
的夹角为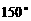 ,
,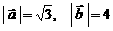 ,则
,则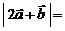 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com