
题目列表(包括答案和解析)
1.设曲线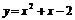 在点M处切线斜率为3,则点M的坐标为
在点M处切线斜率为3,则点M的坐标为
A.(0,-2) B.(1,0) C.(0,0) D.(1,1)
21.已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个顶点,BC过椭圆中心O,且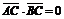 ,|BC|=2|AC|.
,|BC|=2|AC|.
(1)求椭圆方程;
(2)如果椭圆上两点P、Q,使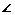 PCQ的平分线垂直AO,是否总存在实数
PCQ的平分线垂直AO,是否总存在实数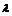 ,使
,使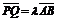 ?请给出说明。
?请给出说明。
20.已知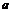 、
、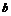 、
、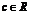 ,
,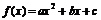 .
.
(1)若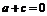 ,
,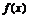 在[-1,1]上的最大值为2,最小值为
在[-1,1]上的最大值为2,最小值为 ,求证:
,求证: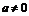 且
且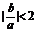 ;
;
(2)若a>0,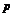 、
、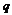 满足
满足 ,且对任意
,且对任意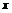 、
、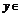 R,均有
R,均有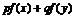 ≥
≥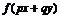 ,求证:
,求证:
0≤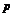 ≤1.
≤1.
19.已知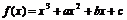 有极大值
有极大值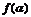 和极小值
和极小值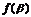 .
.
(1)求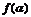 +
+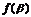 的值;
的值;
(2)设曲线y=f(x)的极值点为A、B,求证:线段AB的中点在y=f(x)上.
18.如图,已知直三棱柱ABC-A1B1C1,AB=AC,F为BB1上一点,
D为BC的中点,且BF=2BD.
(1)当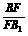 为何值时,对于AD上任意一点E总有EF
为何值时,对于AD上任意一点E总有EF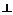 FC1;
FC1;
(2)若A1B1=3,C1F与平面AA1B1B所成角的正弦值为 ,当
,当
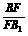 在(1)所给的值时,求三棱柱的体积.
在(1)所给的值时,求三棱柱的体积.
17.{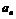 }、{
}、{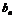 }都是各项为正的数列,对任意的
}都是各项为正的数列,对任意的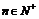 ,都有
,都有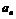 、
、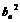 、
、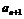 成等差数列,
成等差数列,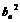 、
、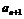 、
、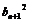 成等比数列.
成等比数列.
(1)试问{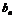 }是否为等差数列,为什么?
}是否为等差数列,为什么?
(2)如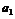 =1,
=1, =
= ,求
,求 ;
;
16.设锐角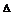 ABC中,
ABC中,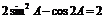 .
.
(1)求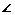 A的大小;
A的大小;
(2)求 取最大值时,
取最大值时,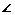 B的大小;
B的大小;
15.已知M={(x,y)|x+y+1>0},N={(x,y)|y=k(x-a)+a},若M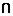 N=
N=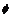 ,则a、k满足的条件是
,则a、k满足的条件是
_______________。
14.设O、A、B、C为平面上四个点, ,
,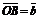 ,
, ,且
,且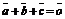 ,
,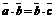
=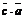 =-1,则
=-1,则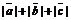 =___________________。
=___________________。
13.如果三棱锥的三个侧面两两垂直,它们的面积分别为6cm2、4cm2和3cm2,那么它的外接球体积是______________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com