
题目列表(包括答案和解析)
2.数列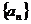 满足
满足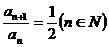 ,a1=1则
,a1=1则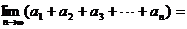 .
.
1.若sina=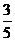 ,a∈(0, π/2),则tga= .
,a∈(0, π/2),则tga= .
21.(本小题满分15分)
已知函数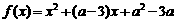 (a为常数).
(a为常数).
(1)如果对任意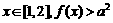 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(2)设实数 满足:
满足: 中的某一个数恰好等于a,且另两个恰为方程
中的某一个数恰好等于a,且另两个恰为方程 的两实根,判断①
的两实根,判断① ,②
,②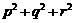 ,③
,③ 是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数
是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数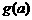 ,并求
,并求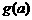 的最小值;
的最小值;
(3)对于(2)中的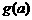 ,设
,设 ,数列
,数列 满足
满足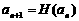
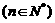 ,且
,且 ,试判断
,试判断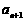 与
与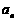 的大小,并证明.
的大小,并证明.
20.(本小题满分14分)
已知点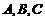 都在椭圆
都在椭圆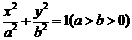 上,
上, 、AC分别过两个焦点
、AC分别过两个焦点 ,当
,当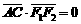 时,有
时,有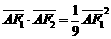 成立.
成立.
(1)求此椭圆的离心率;
(2)设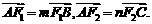 当点A在椭圆上运动时,求证
当点A在椭圆上运动时,求证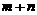 始终是定值.
始终是定值.
19.(本小题满分14分)
数列 的前n项和为
的前n项和为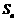 ,且满足
,且满足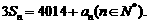
(1)求数列 的通项公式;
的通项公式;
(2)设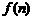 表示该数列的前n项的积,n取何值时,
表示该数列的前n项的积,n取何值时,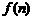 有最大值?
有最大值?
18..(本小题满分15分)
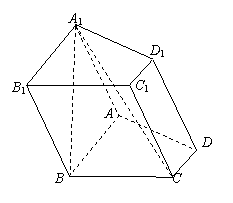
如图,已知四棱柱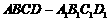 的底面ABCD为直角梯形,
的底面ABCD为直角梯形,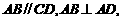 ,
,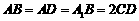 ,侧面
,侧面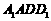 为正方形。
为正方形。
(1)求直线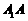 与底面ABCD所成角的大小;
与底面ABCD所成角的大小;
(2)求二面角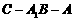 正切值的大小;
正切值的大小;
 (3)在棱
(3)在棱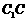 上是否存在一点P,使得
上是否存在一点P,使得 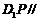 平面
平面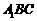 ,若存在,试说明点P的位置;若不存在,请说明理由.
,若存在,试说明点P的位置;若不存在,请说明理由.
17.(本小题满分12分)
已知函数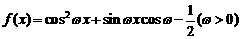 最小正周期为
最小正周期为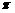 。
。
(1)求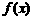 在区间
在区间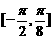 上的最小值;
上的最小值;
(2)求函数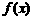 图象上与坐株原点最近的对称中心的坐标。
图象上与坐株原点最近的对称中心的坐标。
16.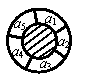 一个同心圆形花坛,分为两部分,如右图,中间小圆部分种
一个同心圆形花坛,分为两部分,如右图,中间小圆部分种
植草坪,周围的圆环分5等份为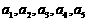 ,种植红、黄、蓝
,种植红、黄、蓝
三色不同的花,要求相邻两部分种植不同颜色的花,则不同的种
植方法种数为 ▲ .
15.甲乙两人投篮中的概率分别为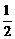 、
、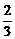 ,现两人各投两次,则投中总数为2的概率为
,现两人各投两次,则投中总数为2的概率为
▲ .
14.已知函数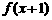 为奇函数,函数
为奇函数,函数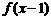 为偶函数,且
为偶函数,且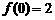 ,则
,则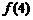 = ▲
= ▲
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com