
题目列表(包括答案和解析)
1.已知不等式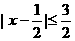 的解集为A,函数
的解集为A,函数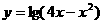 的定义或为B,则
的定义或为B,则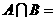
A.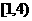 B.
B.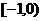 C.
C.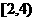 D.
D.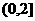
21.已知函数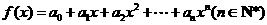 ,记
,记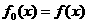 ,
,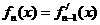 ,且
,且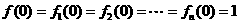 .
.
(1)求数列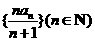 的前
的前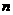 项和;
项和;
(2)解关于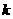 的不等式
的不等式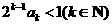 ;
;
(3)证明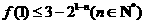 .
.
[解答](1)∵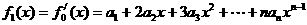 ,
,
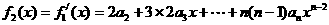 ,
,
……
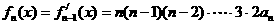 ,
,
∴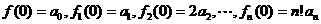 ,
,
而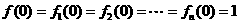 ,
,
∴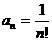 ,∴
,∴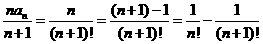
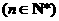 ,
,
∴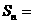
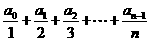
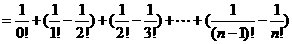
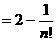 ;
;
(2)当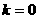 时,
时,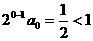 成立,故
成立,故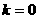 是不等式
是不等式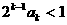 的一个解,
的一个解,
当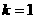 时,
时,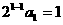 成立,故
成立,故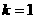 不是不等式
不是不等式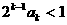 的解,
的解,
当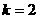 时,
时,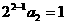 成立,故
成立,故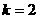 也不是不等式
也不是不等式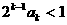 的解,
的解,
当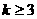 ,
,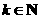 时,∵
时,∵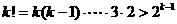 ,
,
∴故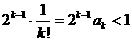 ,故
,故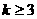 ,
,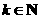 都是不等式
都是不等式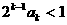 的解,
的解,
综合知所求的解集为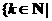
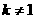 ,且
,且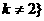 ;
;
(3)∵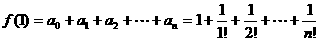 ,
,
且由(2)知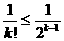 ,
,
∴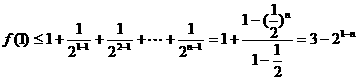 .
.
20.(本小题满分13分)在平面直角坐标系中,已知A1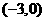 ,A2
,A2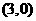 ,P(
,P(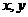 ),M
),M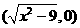 ,O为坐标原点,若实数
,O为坐标原点,若实数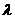 使向量
使向量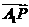 ,
,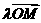 和
和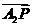 满足
满足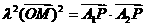 .
.
(1)求点P的轨迹方程,并判断P点的轨迹是怎样的曲线;
(2)当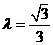 时,过点A1且斜率为1的直线与此时(1)中的曲线相交的另一个交点为B,能否在直线
时,过点A1且斜率为1的直线与此时(1)中的曲线相交的另一个交点为B,能否在直线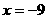 上找到一点C,恰使
上找到一点C,恰使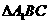 为正三角形?请说明理由.
为正三角形?请说明理由.
[解答](1)由已知可得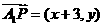 ,
,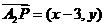 ,
,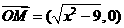 ,且
,且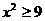 ,∴
,∴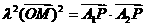 即
即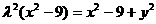 ,
,
即点P的轨迹方程是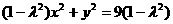 ,
,
当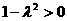 即
即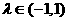 时,有
时,有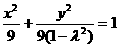 ,
,
此时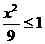 ,∴
,∴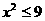 ,综合
,综合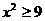 知此时点的轨迹即为两点A1和A2;
知此时点的轨迹即为两点A1和A2;
当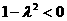 即
即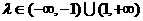 时,方程为
时,方程为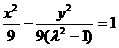 ,
,
此时点P的轨迹是双曲线;
当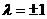 时,方程为
时,方程为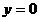 ,且
,且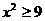 为两条射线;
为两条射线;
(2)过点A1斜率为1的直线方程为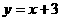 ,
,
当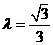 时,曲线方程为
时,曲线方程为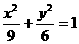 ,其轨迹就是两点A1和A2,
,其轨迹就是两点A1和A2,
此时直线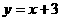 过点A1但不过A2点,∴B点不存在,从而这样的三角形也不存在.
过点A1但不过A2点,∴B点不存在,从而这样的三角形也不存在.
19. (本小题满分12分)如图,已知三棱柱ABC-A1B1C1的棱长都是2,点A1与AB、AC的距离都等于
(本小题满分12分)如图,已知三棱柱ABC-A1B1C1的棱长都是2,点A1与AB、AC的距离都等于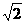 ,且A1E⊥B1B于E,A1F⊥C1C于F.
,且A1E⊥B1B于E,A1F⊥C1C于F.
(1)求证:平面A1EF⊥平面B1BCC1;
(2)求点A到平面B1BCC1的距离;
(3)求平面A1EF与平面A1B1C1所成二面角的大小.
[解答](1)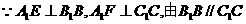 ,∴B1B
,∴B1B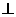 平面A1EF,∴平面A1EF⊥平面B1BCC1;
平面A1EF,∴平面A1EF⊥平面B1BCC1;
(2)由于A1A//平面B1BCC1,
故点A、A1与平面B1BCC1的距离相等.
∵四边形ABB1A1为菱形,故A1E=A1F=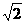 ,
,
∵B1B⊥平面A1EF,EF 平面A1EF,
平面A1EF,
∴BB1⊥EF,从而EF=BC=2,
∴△A1EF是等腰直角三角形,
取EF中点M,则A1M⊥EF,且A1M=1,
从而A1M⊥平面B1BCC1,即A1到平面B1BCC1的距离为1;
(3)设平面A1EF与平面A1B1C1所成的二面角的棱为直线l,取B1C1的中点N,
则A1N⊥B1C1,但B1C1//EF,∴B1C1//平面A1EF,于是B1C1//l,
在△A1B1C1中,A1N=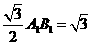 ,∴A1M⊥l,A1N⊥l,
,∴A1M⊥l,A1N⊥l,
即∠MA1N为所求二面角的平面角,
∵A1M⊥平面B1BCC1,∴A1M⊥MN,∴cos∠NA1M=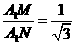 ,
,
故所求二面角的大小为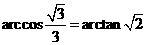 .
.
18.(本小题满分12分)一种电器控制器在出厂时每五件一等品装成一箱,工人在装箱时不小心把两件二等品和3件一等品装入了一箱,为了找出该箱中的二等品,我们把该箱中产品逐一取出进行测试.
(1)求前两次取出都是二等品的概率;
(2)求第二次取出的是二等品的概率;
(3)用随机变量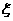 表示第二个二等品被取出时共取出的产品件数,求
表示第二个二等品被取出时共取出的产品件数,求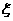 的分布列及数学期望.
的分布列及数学期望.
[解答](1)五件产品逐一取出方法共有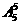 种,
种,
前两次取出都是二等品的方法共有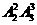 种,
种,
所以前两次取出都是二等品的概率为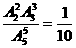
(2)第二次取出是二等品方法共有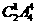 种,
种,
所以第二次取出是二等品的概率是: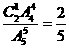 ;
;
(3)依题意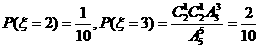 ,
,
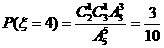 ,
,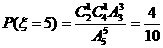
 |
2 |
3 |
4 |
5 |
|
P |
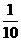 |
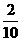 |
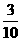 |
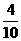 |
所以分布列为:
∴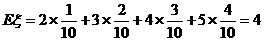 .
.
17.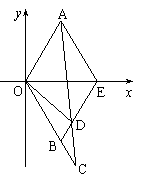 (本小题满分12分)如图,△AOE和△BOE都是边长为1的等边三角形,延长OB到C使|BC|=t(t>0),连AC交BE于D点.
(本小题满分12分)如图,△AOE和△BOE都是边长为1的等边三角形,延长OB到C使|BC|=t(t>0),连AC交BE于D点.
(1)用t表示向量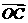 和
和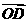 的坐标;
的坐标;
(2)求向量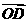 和
和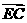 的夹角的大小;
的夹角的大小;
(3)求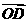
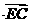 的取值范围。
的取值范围。
[解答](1)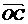 =((t+1),-(t+1)),
=((t+1),-(t+1)),
∵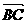 =t
=t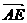 ,∴
,∴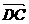 =t
=t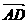 ,
,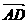 =
=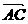 ,又
,又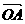 =(,),
=(,),
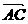 =
=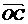 -
-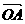 =(t,-(t+2));∴
=(t,-(t+2));∴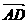 =(,-),
=(,-),
∴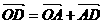 =(,-);
=(,-);
(2)∵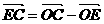 =(,-),
=(,-),
∴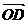 ·
·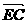 =·+·=,
=·+·=,
又∵|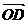 |·|
|·|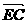 |=
|=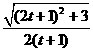 ·
·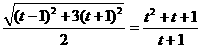 ,
,
∴cos<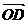 ,
,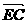 >==,∴向量
>==,∴向量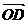 与
与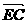 的夹角为60°;
的夹角为60°;
(3)由(2)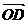 ·
·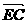 =
=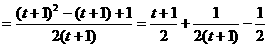 ,
,
∴ ·
·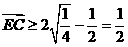 ,且等号不能取得,
,且等号不能取得,
∴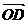 ·
·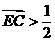 ,所求范围是
,所求范围是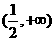 。
。
16.已知函数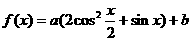 .
.
(1)当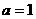 时,求函数
时,求函数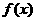 的单调递增区间;
的单调递增区间;
(2)当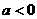 且
且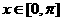 时,函数
时,函数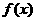 的值域为
的值域为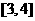 ,求
,求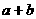 的值.
的值.
[解答]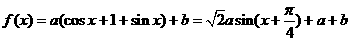 ,
,
(1)当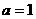 时,
时,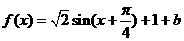 ,
,
∴当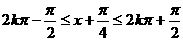 (
(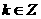 )时
)时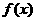 是增函数,
是增函数,
∴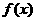 的单调递增区间是
的单调递增区间是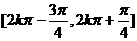 (
(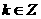 );
);
(2)由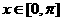 得
得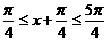 ,
,
∴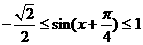 ,
,
∵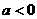 ,∴当
,∴当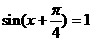 时,
时,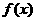 取得最小值为3,
取得最小值为3,
而当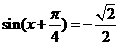 时,
时,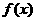 取得最大值为4,
取得最大值为4,
即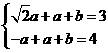 ,解得
,解得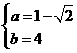 ,∴
,∴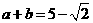 .
.
15.对大于2或等于2的自然数 的
的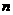 次幂进行如下方式的“分裂”:
次幂进行如下方式的“分裂”:
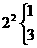 ,
,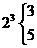 ,
,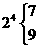 ;
;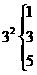 ,
,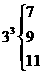 ,
,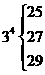 ,
,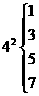 ,…
,…
则对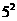 进行类似的“分裂”时,“分裂”中的最大的数是____________;若已知
进行类似的“分裂”时,“分裂”中的最大的数是____________;若已知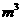 在“分裂”中的最小数是21,则
在“分裂”中的最小数是21,则 的值为______________.
的值为______________.
[答案]9,5
提示:由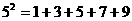 得
得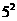 “分裂”中的最大的数是9;又
“分裂”中的最大的数是9;又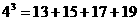 ,而
,而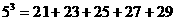 ,故知若
,故知若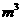 在“分裂”中的最小数是21,则
在“分裂”中的最小数是21,则 的值为5.
的值为5.
14.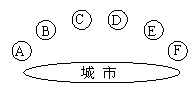 某市为改善投资环境,计划对城郊结合部如图所示的A、B、C、D、E、F六个区域进行治理,第一期工程拟从这六个区域中选取三个区域,但要求至多有两个区域相邻,则不同的选取方法共有____________种(用数字作答).其中区域A在第一期得到治理的概率是_______________.
某市为改善投资环境,计划对城郊结合部如图所示的A、B、C、D、E、F六个区域进行治理,第一期工程拟从这六个区域中选取三个区域,但要求至多有两个区域相邻,则不同的选取方法共有____________种(用数字作答).其中区域A在第一期得到治理的概率是_______________.
[答案]16,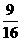
提示:分两类,第一类,恰有两个区域相邻--当AB或EF相邻时各有3种,当BC、CD、DE相邻时各有2种;三个区域都不相邻--有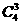 种方法;故共有16种方法.
种方法;故共有16种方法.
其中含有A的方法有ABD(E、F),ACD(DE、EF、DF)和ACE(F)9种,故所求概率为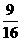 .
.
13.设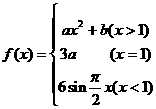 ,若
,若 在
在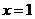 处连续,则
处连续,则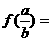 __________.
__________.
[答案]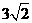
提示:当点处的极限值等于其函数值,∴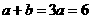 ,∴
,∴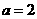 ,
,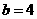 ,故得
,故得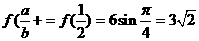 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com