
题目列表(包括答案和解析)
1. 某班数学兴趣小组有男生和女生各3名,现从中任选2名学生去参加校数学竞赛,求
(I) 恰有一名参赛学生是男生的概率;
(II)至少有一名参赛学生是男生的概率;
(Ⅲ)至多有一名参赛学生是男生的概率。
解:基本事件的种数为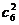 =15种
=15种
(Ⅰ)恰有一名参赛学生是男生的基本事件有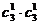 =9种
=9种  所求事件概率P1=
所求事件概率P1=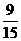 =0.6
=0.6
(Ⅱ)至少有一名参赛学生是男生这一事件是由两类事件构成的,即恰有一名参赛学生是男生和两名参赛学生都是男生, 所求事件概率P2=
所求事件概率P2=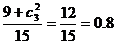
(Ⅲ)至多有一名参赛学生是男生这一事件也是由两类事件构成的,即参赛学生没有男生和恰有一名参赛学生是男生, 所求事件概率P3=
所求事件概率P3=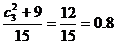
23、如图,用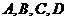 表示四类不同的元件连接成
表示四类不同的元件连接成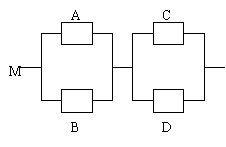 系统
系统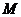 。当元件
。当元件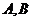 至少有一个正常工作且元件
至少有一个正常工作且元件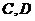 至少有一个正常工作时,系统
至少有一个正常工作时,系统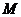 正常工作。已知元件
正常工作。已知元件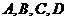 正常工作的概率依次为0.5,0.6,0.7,0.8,求元件连接成的系统
正常工作的概率依次为0.5,0.6,0.7,0.8,求元件连接成的系统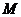 正常工作
正常工作
的概率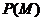 .
.
22、为了测试甲、乙两名射击运动员的射击水平,让他们各向目标靶射出10次,其中甲击中目标7次,乙击中目标6次,若再让甲、乙两人各自向目标靶射击3次,求:
(1)甲运动员恰好击中目标2次的概率是多少?
(2)两名运动员都恰好击中目标2次的概率是多少?(结果保留两个有效数字).
21、某次有奖竞猜活动中,主持人准备了A、B两个相互独立的问题, 并且宣布:观众答对问题A可获奖金a元,答对问题B可获奖金2a元;先答哪个题由观众自由选择;只有第1个问题答对,才能再答第2个问题,否则中止答题。若你被选为幸运观众,且假设你答对问题A、B的概率分别为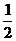 、
、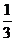 。你觉得应先回答哪个问题才能使你获得奖金的期望较大?说明理由。
。你觉得应先回答哪个问题才能使你获得奖金的期望较大?说明理由。
20、袋子内装有大小相同的15个小球,其中有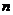 个红球,5个黄球,其余为白球.
个红球,5个黄球,其余为白球.
(1)从中任意摸出2个小球,求得到2个球都是黄球的概率;
(2)如果从中任意摸出2个小球,得到都是红球或黄球的概率为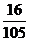 ,求红球的个数。
,求红球的个数。
19、有一个4×5×6的长方体, 它的六个面上均涂上颜色. 现将这个长方体锯成120个1×1 ×1的小正方体, 从这些小正方体中随机地任取1个.
(I) 设小正方体涂上颜色的面数为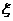 , 求
, 求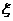 的分布列和数学期望.
的分布列和数学期望.
(II) 如每次从中任取一个小正方体,
确定涂色的面数后, 再放回, 连续抽取6次, 设恰好取到两面涂有颜色的小正方体次数为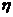 . 求
. 求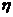 的数学期望.
的数学期望.
18、设离散型随机变量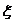 所有可能值为1,2,3,4,且
所有可能值为1,2,3,4,且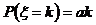 (
(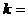 1,2,3,4)。
1,2,3,4)。
(1)求常数a的值;(2)求随机变量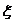 的分布列;(3)求
的分布列;(3)求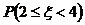 。
。
17、甲、乙两支足球队90分钟踢成平局,加时赛30分钟后仍成平局.现决定每队各派5名队员,每人射一个点球来决定胜负.设甲、乙两队每个队员的点球命中率均为0.5.
(1)若不考虑乙队,求甲队仅有3名队员点球命中,且其中恰有两名队员连续命中的概率;
(2)求甲、乙两队各射完5个点球后,再次出现平局的概率.
16、已知随机变量ξ的分布列如右表:
设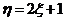 ,则
,则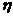 的期望值
的期望值
Eη= 。
15、 若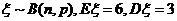 ,则
,则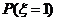 的值为:
A、
的值为:
A、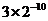 B、
B、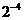 C、
C、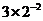 D、
D、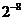
|
ξ |
1 |
2 |
3 |
|
p |
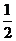 |
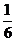 |
b |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com