
题目列表(包括答案和解析)
(二)直线方程
1. 直线方程:
(1)点斜式:
y-y0=k(x-x0)(已知:点P0(x0,y0),斜率k)
(2)斜截式:
y=kx+b(已知:斜率k及纵截距b)
(3)两点式:
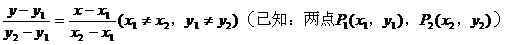
(4)截距式:
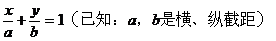
(5)一般式:
Ax+By+C=0(A、B不同时为0)
2. 两条直线的位置关系:
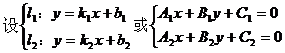
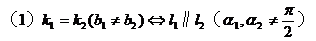
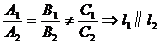
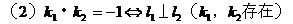
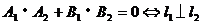
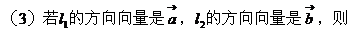
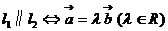
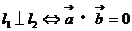
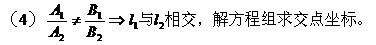
(5)夹角θ:按逆时针方向从l1转到l2所成的角,叫做l1到l2的角。
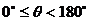
两条直线相交所成的锐角或直角,叫做两条直线的夹角θ。
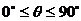


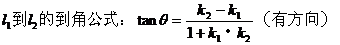
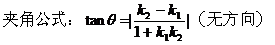
3. 点到直线的距离公式:
P(x0,y0)是已知点,l:Ax+By+C=0是已知直线,则
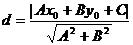
4. 对称点:
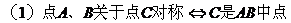
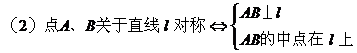
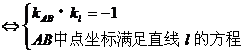
5. 直线系方程:
(1)过定点(x1,y1)的直线系方程:
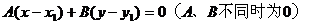
(2)平行于直线Ax+By+C=0的直线系方程:
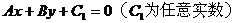
(3)垂直于直线Ax+By+C=0的直线系方程:
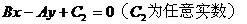
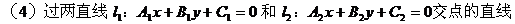
系方程:
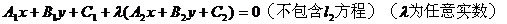
(一)基本公式
1. 有向线段
设P1(x1,y1),P2(x2,y2)
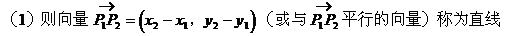

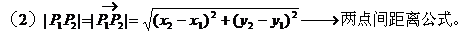
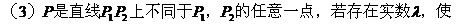

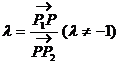
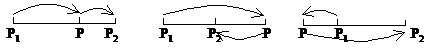
P为内分点,λ>0;P为外分点,λ<0。
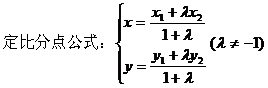
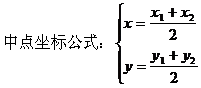
例如:设△ABC,A(x1,y1),B(x2,y2),C(x3,y3)
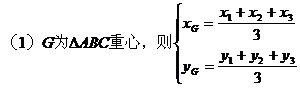
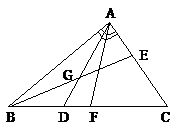
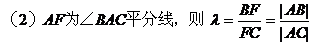
2. 直线l的倾斜角α(直线向上的方向与x轴的正方向所成的最小正角)
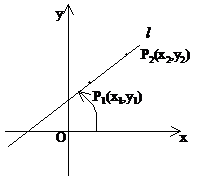
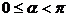

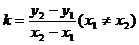
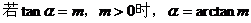
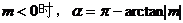
3. 了解二元一次不等式表示平面区域,了解线性规划的意义,并会简单应用。
2. 掌握两直线平行、垂直的条件;掌握两条直线所成角的公式和点到直线的距离公式。
直线方程及其应用
[教学要求]
1. 理解直线斜率的概念,掌握过两点的直线的斜率公式,掌握直线方程的点斜式、两点式、一般式,并能根据条件熟练求出直线方程。
22.(本题满分18分)
已知函数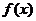 是定义在
是定义在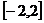 上的奇函数,当
上的奇函数,当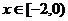 时,
时,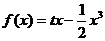 (
(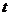 为常数)。
为常数)。
(1)求函数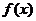 的解析式;
的解析式;
(2)当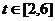 时,求
时,求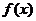 在
在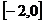 上的最小值,及取得最小值时的
上的最小值,及取得最小值时的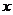 ,并猜想
,并猜想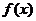 在
在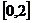 上的单调递增区间(不必证明);
上的单调递增区间(不必证明);
(3)当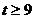 时,证明:函数
时,证明:函数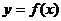 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线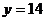 上。
上。
解:(1)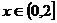 时,
时,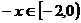 , 则
, 则 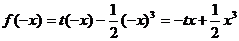
∵函数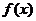 是定义在
是定义在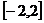 上的奇函数,即
上的奇函数,即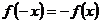
∴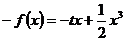 ,即
,即 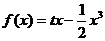 ,又可知
,又可知 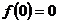
∴函数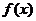 的解析式为
的解析式为 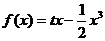 ,
,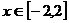
(2)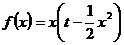 ,∵
,∵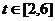 ,
,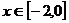 ,∴
,∴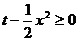
∵ 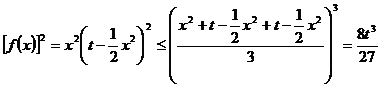
∴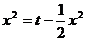 ,即
,即 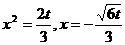
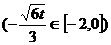 时,
时,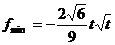 。
。
猜想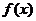 在
在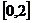 上的单调递增区间为
上的单调递增区间为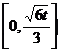 。
。
(3)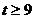 时,任取
时,任取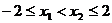 ,∵
,∵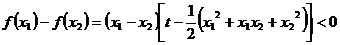
∴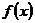 在
在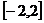 上单调递增,即
上单调递增,即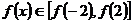 ,即
,即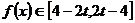
∵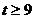 ,∴
,∴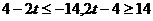 ,∴
,∴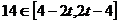
∴当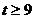 时,函数
时,函数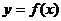 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线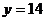 上。
上。
21.(本题满分16分)
对数列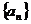 ,规定
,规定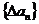 为数列
为数列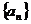 的一阶差分数列,其中
的一阶差分数列,其中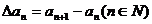 。
。
对自然数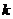 ,规定
,规定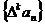 为
为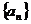 的
的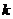 阶差分数列,其中
阶差分数列,其中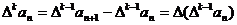 。
。
(1)已知数列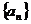 的通项公式
的通项公式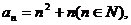 ,试判断
,试判断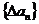 ,
,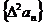 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?
(2)若数列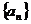 首项
首项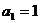 ,且满足
,且满足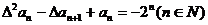 ,求数列
,求数列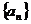 的通项公式。
的通项公式。
(3)对(2)中数列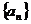 ,是否存在等差数列
,是否存在等差数列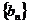 ,使得
,使得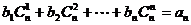 对一切自然
对一切自然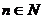 都成立?若存在,求数列
都成立?若存在,求数列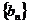 的通项公式;若不存在,则请说明理由。
的通项公式;若不存在,则请说明理由。
解:(1)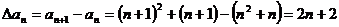 ,∴
,∴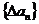 是首项为4,公差为2的等差数列。
是首项为4,公差为2的等差数列。
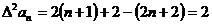
∴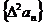 是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列。
是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列。
(2)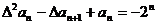 ,即
,即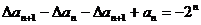 ,即
,即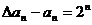 ,∴
,∴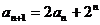
∵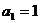 ,∴
,∴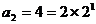 ,
,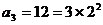 ,
,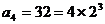 ,猜想:
,猜想: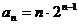
证明:ⅰ)当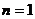 时,
时,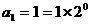 ;
;
ⅱ)假设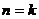 时,
时,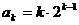
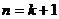 时,
时,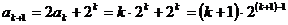 结论也成立
结论也成立
∴由ⅰ)、ⅱ)可知,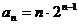
(3)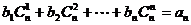 ,即
,即 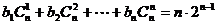
∵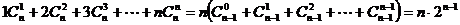
∴存在等差数列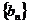 ,
,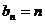 ,使得
,使得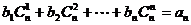 对一切自然
对一切自然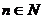 都成立。
都成立。
20.(本题满分14分)
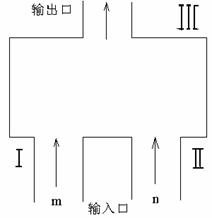 如图,一个计算装置有两个数据输入口Ⅰ、Ⅱ与一个运算结果输出口Ⅲ,当Ⅰ、Ⅱ分别输入正整数
如图,一个计算装置有两个数据输入口Ⅰ、Ⅱ与一个运算结果输出口Ⅲ,当Ⅰ、Ⅱ分别输入正整数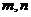 时,输出结果记为
时,输出结果记为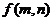 ,且计算装置运算原理如下:
,且计算装置运算原理如下:
①
若Ⅰ、Ⅱ分别输入1,则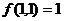 ;②若Ⅰ输入固定的正整数,
;②若Ⅰ输入固定的正整数,
Ⅱ输入的正整数增大1,则输出结果比原来增大3;③若Ⅱ输入1,
Ⅰ输入正整数增大1,则输出结果为原来3倍。
试求:
(1)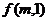 的表达式
的表达式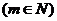 ;(2)
;(2)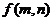 的表达式
的表达式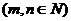 ;
;
(3)若Ⅰ、Ⅱ都输入正整数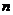 ,则输出结果
,则输出结果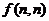 能否为2005?
能否为2005?
若能,求出相应的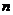 ;若不能,则请说明理由。
;若不能,则请说明理由。
解:(1)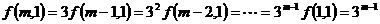
(2)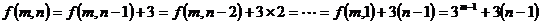
(3)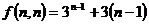 ,∵
,∵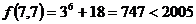 ,
,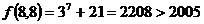
∴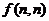 输出结果不可能为
输出结果不可能为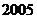 。
。
19.(本题满分14分)
已知关于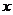 的不等式
的不等式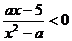 的解集为
的解集为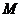 。
。
(1)当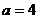 时,求集合
时,求集合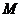 ;
;
(2)若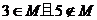 ,求实数
,求实数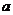 的取值范围。
的取值范围。
解:(1)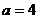 时,不等式为
时,不等式为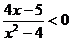 ,解之,得
,解之,得 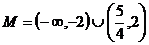
(2)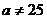 时,
时,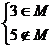
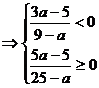
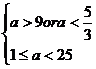
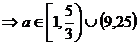
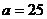 时,不等式为
时,不等式为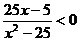 , 解之,得
, 解之,得 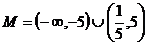 ,
,
则 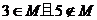 , ∴
, ∴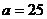 满足条件
满足条件
综上,得 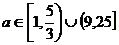 。
。
18.(本题满分12分)
设复数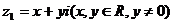 ,复数
,复数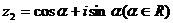 ,且
,且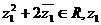 在复平面上所对应点在直线
在复平面上所对应点在直线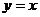 上,求
上,求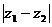 的取值范围。
的取值范围。
解: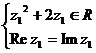
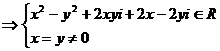
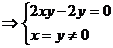
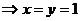
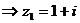
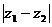
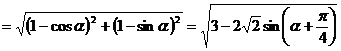 ∴
∴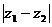
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com