
题目列表(包括答案和解析)
21、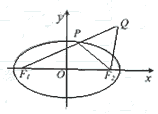 (Ⅰ)证法一:设点P的坐标为
(Ⅰ)证法一:设点P的坐标为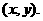
由P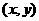 在椭圆上,得
在椭圆上,得
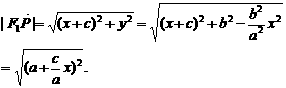
由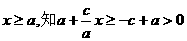 ,所以
,所以 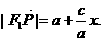 ………………………3分
………………………3分
证法二:设点P的坐标为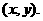 记
记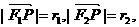
则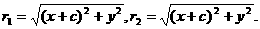
由
证法三:设点P的坐标为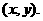 椭圆的左准线方程为
椭圆的左准线方程为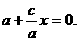
由椭圆第二定义得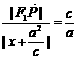 ,即
,即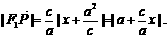
由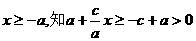 ,所以
,所以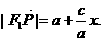 …………………………3分
…………………………3分
(Ⅱ)解法一:设点T的坐标为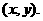
当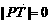 时,点(
时,点(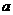 ,0)和点(-
,0)和点(-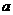 ,0)在轨迹上.
,0)在轨迹上.
当| 时,由
时,由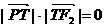 ,得
,得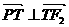 .
.
又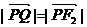 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
在△QF1F2中,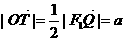 ,所以有
,所以有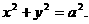
综上所述,点T的轨迹C的方程是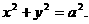 …………………………7分
…………………………7分
解法二:设点T的坐标为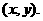 当
当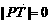 时,点(
时,点(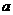 ,0)和点(-
,0)和点(-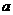 ,0)在轨迹上.
,0)在轨迹上.
当| 时,由
时,由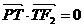 ,得
,得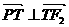 .
.
又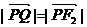 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
设点Q的坐标为(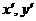 ),则
),则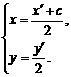
因此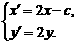 ①
①
由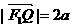 得
得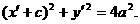 ②
②
将①代入②,可得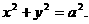
综上所述,点T的轨迹C的方程是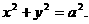 ……………………7分
……………………7分
|
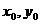 )使S=
)使S=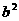 的充要条件是
的充要条件是
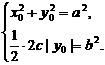
由③得 ,由④得
,由④得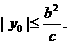 所以,当
所以,当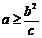 时,存在点M,使S=
时,存在点M,使S=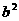 ;
;
当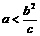 时,不存在满足条件的点M.………………………11分
时,不存在满足条件的点M.………………………11分
当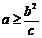 时,
时,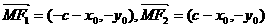 ,
,
由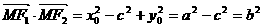 ,
,
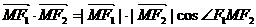 ,
,
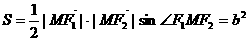 ,得
,得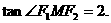
解法二:C上存在点M(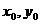 )使S=
)使S=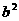 的充要条件是
的充要条件是
|
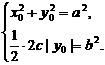
由④得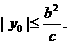 上式代入③得
上式代入③得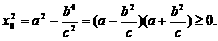
于是,当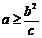 时,存在点M,使S=
时,存在点M,使S=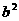 ;
;
当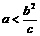 时,不存在满足条件的点M.………………………11分
时,不存在满足条件的点M.………………………11分
当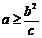 时,记
时,记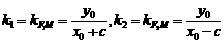 ,
,
由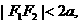 知
知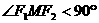 ,所以
,所以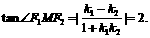 …………14分
…………14分
20、 [解](1)由已知可得点A(-6,0),F(0,4)
设点P(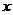 ,
,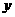 ),则
),则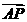 ={
={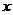 +6,
+6, 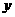 },
},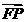 ={
={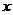 -4,
-4, 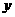 },由已知可得
},由已知可得
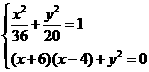
则2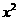 +9
+9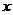 -18=0,
-18=0, 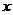 =
=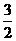 或
或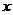 =-6.
=-6.
由于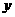 >0,只能
>0,只能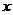 =
=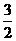 ,于是
,于是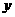 =
=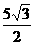 .
.
∴点P的坐标是(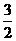 ,
,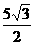 )
)
(2) 直线AP的方程是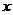 -
-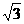
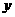 +6=0.
+6=0.
设点M( ,0),则M到直线AP的距离是
,0),则M到直线AP的距离是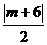 .
.
于是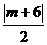 =
=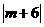 ,又-6≤
,又-6≤ ≤6,解得
≤6,解得 =2.
=2.
椭圆上的点(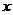 ,
,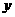 )到点M的距离
)到点M的距离 有
有
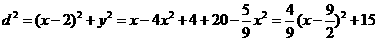 ,
,
由于-6≤ ≤6, ∴当
≤6, ∴当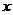 =
=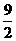 时,d取得最小值
时,d取得最小值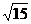
19、解:(1)设双曲线的渐近线为y=kx,由d=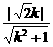 =1,解得k=±1.
=1,解得k=±1.
即渐近线为y=±x,又点A关于y=x对称点的坐标为(0,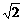 ).
).
∴a=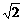 =b,所求双曲线C的方程为x2-y2=2.
=b,所求双曲线C的方程为x2-y2=2.
(2)设直线l:y=k(x-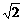 )(0<k<1
)(0<k<1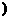 ,依题意B点在平行的直线l′上,
,依题意B点在平行的直线l′上,
且l与l′间的距离为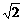 .
.
设直线l′:y=kx+m,应有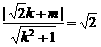 ,化简得m2+2
,化简得m2+2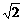 km=2. ②
km=2. ②
把l′代入双曲线方程得(k2-1)x2+2mkx+m2-2=0,
由Δ=4m2k2-4(k2-1)(m2-2)=0.可得m2+2k2=2 ③
②、③两式相减得k=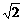 m,代入③得m2=
m,代入③得m2=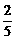 ,解设m=
,解设m=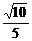 ,k=
,k=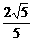 ,
,
此时x=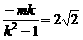 ,y=
,y=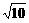 .故B(2
.故B(2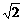 ,
,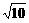 ).
).
18、解:(1)如图,设双曲线方程为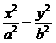 =1.由已知得
=1.由已知得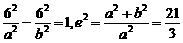 ,解得a2=9,b2=12.
,解得a2=9,b2=12.
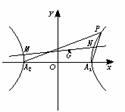
所以所求双曲线方程为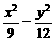 =1.
=1.
(2)P、A1、A2的坐标依次为(6,6)、(3,0)、(-3,0),
∴其重心G的坐标为(2,2)
假设存在直线l,使G(2,2)平分线段MN,设M(x1,y1),N(x2,y2).则有
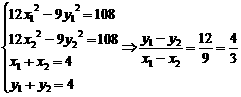 ,∴kl=
,∴kl=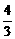
∴l的方程为y=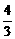 (x-2)+2,
(x-2)+2,
由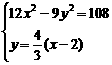 ,消去y,整理得x2-4x+28=0.
,消去y,整理得x2-4x+28=0.
∵Δ=16-4×28<0, ∴所求直线l不存在.
17、解:(1)设直线l的方程为:y=x-a,代入抛物线方程得(x-a)2=2px,即x2-2(a+p)x+a2=0
∴|AB|=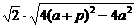 ≤2p.∴4ap+2p2≤p2,即4ap≤-p2
≤2p.∴4ap+2p2≤p2,即4ap≤-p2
又∵p>0,∴a≤-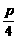 .
.
(2)设A(x1,y1)、B(x2,y2),AB的中点 C(x,y),
由(1)知,y1=x1-a,y2=x2-a,x1+x2=2a+2p,
则有x=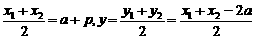 =p.
=p.
∴线段AB的垂直平分线的方程为y-p=-(x-a-p),从而N点坐标为(a+2p,0)?
点N到AB的距离为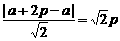
从而S△NAB=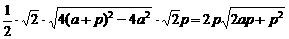
当a有最大值-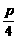 时,S有最大值为
时,S有最大值为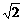 p2.
p2.
11、x+2y-4=0 12、 13、y=8x-15. 14、18或50 15、2 16、
C B C C A C D D B B
21、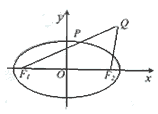 已知椭圆
已知椭圆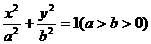 的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足
的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足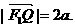 点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足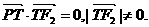
(Ⅰ)设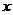 为点P的横坐标,证明
为点P的横坐标,证明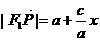 ;
;
(Ⅱ)求点T的轨迹C的方程;
(Ⅲ)试问:在点T的轨迹C上,是否存在点M,
使△F1MF2的面积S=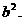 若存在,求∠F1MF2
若存在,求∠F1MF2
的正切值;若不存在,请说明理由.
[2006年高考二轮复习专题讲义之针对训练]
解析几何专题--解析几何的综合运用同步训练答案
20、点A、B分别是椭圆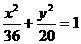 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于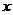 轴上方,
轴上方,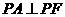 。
。
(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于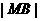 ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离 的最小值。
的最小值。
19、已知双曲线C的两条渐近线都过原点,且都以点A(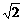 ,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称.
,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称.
(1)求双曲线C的方程.
(2)设直线l过点A,斜率为k,当0<k<1时,双曲线C的上支上有且仅有一点B到直线l的距离为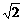 ,试求k的值及此时B点的坐标.
,试求k的值及此时B点的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com