
题目列表(包括答案和解析)
4.等比数列中,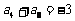 ,则
,则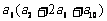 的值为( ).
的值为( ).
A.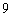 B.
B.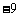 C.
C.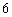 D.
D.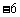
3.“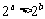 ”是 “
”是 “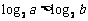 ”的( ).
”的( ).
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2.(文)在检查产品尺寸过程中,将其尺寸分成若干组,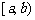 是其中一组,抽查出的个体在该组上频率
是其中一组,抽查出的个体在该组上频率
为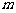 ,该组上的直方图的高为
,该组上的直方图的高为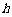 ,则
,则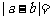 ( ).
( ).
A.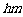 B.
B. 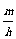 C.
C. 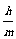 D.
D.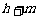
(理)在某学校举行的数学竞赛中,全体参赛学生的成绩近似服从正态分布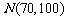 .已知成绩在
.已知成绩在
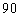 分以上(含
分以上(含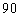 分)的学生有
分)的学生有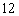 名,则此次竞赛的学生总人数约( )人.
名,则此次竞赛的学生总人数约( )人.
(参考数据: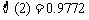 )
)
A.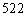 B.
B.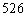 C.
C.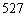 D.
D.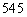
1.已知非空集合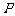 、
、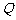 、
、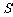 都是全集
都是全集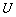 的子集,且
的子集,且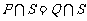 ,则( ).
,则( ).
A.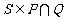 B.
B.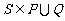 C.
C.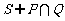 D.
D.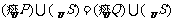
22.已知曲线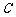 :
: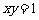 ,过
,过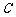 上一点
上一点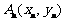 作一斜率为
作一斜率为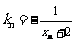 的直线交曲线
的直线交曲线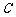 于另一点
于另一点
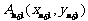 ,点列
,点列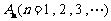 的横坐标构成数列
的横坐标构成数列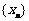 ,其中
,其中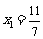 .
.
⑴求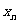 与
与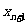 的关系式; ⑵求证:
的关系式; ⑵求证: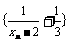 是等比数列;
是等比数列;
⑶求证: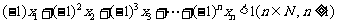
21.已知直线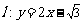 与椭圆
与椭圆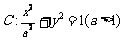 交于
交于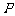 、
、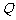 两点,以
两点,以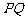 为直径的圆过椭圆
为直径的圆过椭圆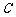 的
的
右顶点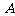 .
.
(Ⅰ)设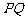 中点
中点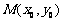 ,
,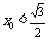 ; (Ⅱ)求椭圆
; (Ⅱ)求椭圆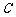 方程.
方程.
20.(文)已知函数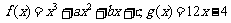 ,若
,若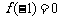 ,且
,且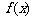 的图象在点
的图象在点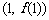 处
处
的切线方程为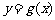 .
.
(Ⅰ)求实数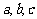 的值;
(Ⅱ)求函数
的值;
(Ⅱ)求函数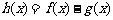 的单调区间.
的单调区间.
(理)已知函数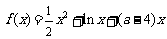 在上是增函数.
在上是增函数.
(Ⅰ)求实数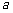 取值范围;
取值范围;
(Ⅱ)在(Ⅰ)的结论下,设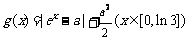 ,求函数
,求函数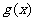 的最小值.
的最小值.
19.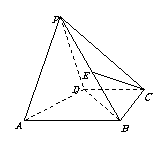 如图,在四棱锥
如图,在四棱锥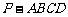 中,平面
中,平面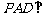 平面
平面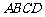 ,
, ,
,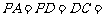
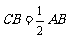 ,
,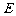 是
是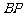 的中点. (Ⅰ)求证:
的中点. (Ⅰ)求证: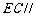 平面
平面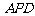 ;
;
(Ⅱ)求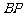 与平面
与平面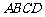 所成角的正切值;
所成角的正切值;
(Ⅲ)求二面角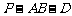 的大小.
的大小.
18.(文)已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为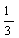 ,某植物研究所分两个
,某植物研究所分两个
小组分别独立开展该种子的发芽实验,每次实验一粒种子,假定某次实验种子发芽则称该次实验
是成功的,如果种子没有发芽,则称该次实验是失败的.
⑴第一小组做了三次实验,求至少有两次实验成功的概率;
⑵第二小组进行试验,到成功了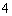 次为止,求在第四次成功之前共有三次失败,且恰有两次连续
次为止,求在第四次成功之前共有三次失败,且恰有两次连续
失败的概率.
(理)小张有一只放在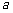 个红球,
个红球,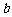 个黄球,
个黄球,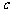 个白球的箱子,且
个白球的箱子,且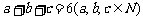 .小刘有一只
.小刘有一只
放有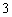 个红球,
个红球,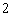 黄球,
黄球,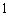 个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同
个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同
色时小张胜,异色时小刘胜.
⑴用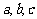 表示小张获胜的概率;
表示小张获胜的概率;
⑵若又规定当小张取红、黄、白球而胜得分分别为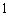 分、
分、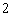 分、
分、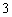 分,否则得
分,否则得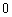 分,求小张得分的
分,求小张得分的
期望的最大值及此时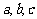 的值.
的值.
17.(文)已知函数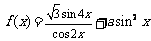 在
在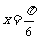 取到最大值.
取到最大值.
⑴求函数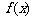 的定义域; ⑵求实数
的定义域; ⑵求实数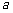 的值.
的值.
(理)函数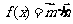 ,其中
,其中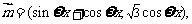
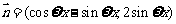 其中
其中
 ,若
,若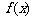 相邻两对称轴间的距离不小于
相邻两对称轴间的距离不小于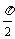 . (Ⅰ)求
. (Ⅰ)求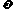 的取值范围;
的取值范围;
(Ⅱ)在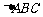 中,
中,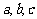 分别是角
分别是角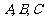 的对边,
的对边,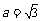 ,
,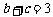 .当
.当 最大时,
最大时,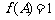 ,
,
求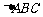 的面积.
的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com