
题目列表(包括答案和解析)
(一)方法总结
导数是中学限选内容中较为重要的知识,由于其应用的广泛性,为我们解决所学过的有关函数问题提供了一般性方法,是解决实际问题强有力的工具。导数的概念及其运算是导数应用的基础,是高考重点考查的对象。要牢记导数公式,熟练应用导数公式求函数的导数,掌握求导数的方法。应用导数解决实际问题的关键是要建立恰当的数学模型,了解导数概念的实际背景。应用导数求函数最值及极值的方法在例题讲解中已经有了比较详细的叙述。
考点一:求导公式。
例1. 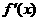 是
是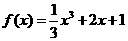 的导函数,则
的导函数,则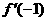 的值是
。
的值是
。
解析: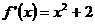 ,所以
,所以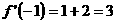
答案:3
点评:本题考查多项式的求导法则。
考点二:导数的几何意义。
例2. 已知函数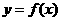 的图象在点
的图象在点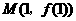 处的切线方程是
处的切线方程是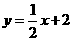 ,则
,则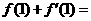 。
。
解析:因为 ,所以
,所以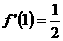 ,由切线过点
,由切线过点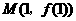 ,可得点M的纵坐标为
,可得点M的纵坐标为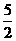 ,所以
,所以 ,所以
,所以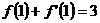
答案:3
例3.曲线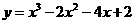 在点
在点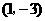 处的切线方程是
。
处的切线方程是
。
解析: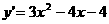 ,
, 点
点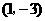 处切线的斜率为
处切线的斜率为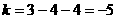 ,所以设切线方程为
,所以设切线方程为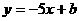 ,将点
,将点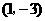 带入切线方程可得
带入切线方程可得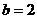 ,所以,过曲线上点
,所以,过曲线上点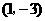 处的切线方程为:
处的切线方程为: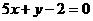
答案: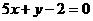
点评:以上两小题均是对导数的几何意义的考查。
考点三:导数的几何意义的应用。
例4.已知曲线C: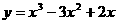 ,直线
,直线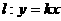 ,且直线
,且直线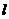 与曲线C相切于点
与曲线C相切于点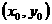
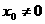 ,求直线
,求直线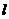 的方程及切点坐标。
的方程及切点坐标。
解析: 直线过原点,则
直线过原点,则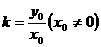 。由点
。由点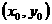 在曲线C上,则
在曲线C上,则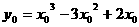 ,
,
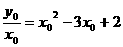 。又
。又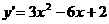 ,
, 在
在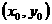 处曲线C的切线斜率为
处曲线C的切线斜率为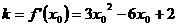 ,
,
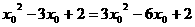 ,整理得:
,整理得: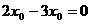 ,解得:
,解得: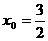 或
或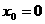 (舍),此时,
(舍),此时,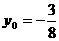 ,
,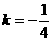 。所以,直线
。所以,直线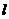 的方程为
的方程为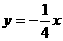 ,切点坐标是
,切点坐标是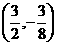 。
。
答案:直线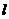 的方程为
的方程为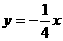 ,切点坐标是
,切点坐标是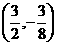
点评:本小题考查导数几何意义的应用。解决此类问题时应注意“切点既在曲线上又在切线上”这个条件的应用。函数在某点可导是相应曲线上过该点存在切线的充分条件,而不是必要条件。
考点四:函数的单调性。
例5.已知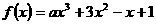 在R上是减函数,求
在R上是减函数,求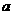 的取值范围。
的取值范围。
解析:函数 的导数为
的导数为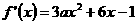 。对于
。对于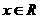 都有
都有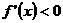 时,
时, 为减函数。由
为减函数。由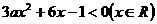 可得
可得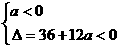 ,解得
,解得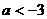 。所以,当
。所以,当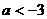 时,函数
时,函数 对
对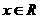 为减函数。
为减函数。
2
当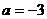 时,
时,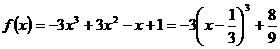 。
。
由函数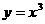 在R上的单调性,可知当
在R上的单调性,可知当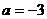 是,函数
是,函数 对
对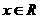 为减函数。
为减函数。
7
当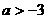 时,函数
时,函数 在R上存在增区间。所以,当
在R上存在增区间。所以,当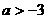 时,函数
时,函数 在R上不是单调递减函数。
在R上不是单调递减函数。
综合(1)(2)(3)可知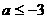 。
。
答案: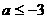
点评:本题考查导数在函数单调性中的应用。对于高次函数单调性问题,要有求导意识。
考点五:函数的极值。
例6. 设函数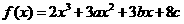 在
在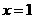 及
及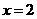 时取得极值。
时取得极值。
(1)求a、b的值;
(2)若对于任意的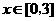 ,都有
,都有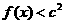 成立,求c的取值范围。
成立,求c的取值范围。
解析:(1)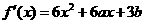 ,因为函数
,因为函数 在
在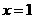 及
及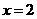 取得极值,则有
取得极值,则有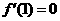 ,
,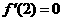 .即
.即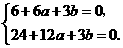 ,解得
,解得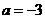 ,
,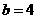 。
。
(2)由(Ⅰ)可知, ,
,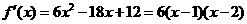 。
。
当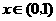 时,
时,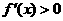 ;当
;当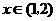 时,
时,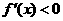 ;当
;当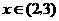 时,
时,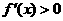 。所以,当
。所以,当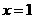 时,
时, 取得极大值
取得极大值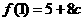 ,又
,又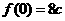 ,
,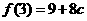 。则当
。则当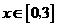 时,
时, 的最大值为
的最大值为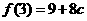 。因为对于任意的
。因为对于任意的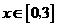 ,有
,有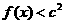 恒成立,
恒成立,
所以 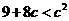 ,解得
,解得 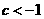 或
或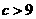 ,因此
,因此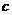 的取值范围为
的取值范围为 。
。
答案:(1)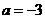 ,
,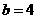 ;(2)
;(2) 。
。
点评:本题考查利用导数求函数的极值。求可导函数 的极值步骤:①求导数
的极值步骤:①求导数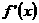 ;
;
②求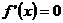 的根;③将
的根;③将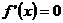 的根在数轴上标出,得出单调区间,由
的根在数轴上标出,得出单调区间,由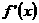 在各区间上取值的正负可确定并求出函数
在各区间上取值的正负可确定并求出函数 的极值。
的极值。
考点六:函数的最值。
例7. 已知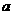 为实数,
为实数, 。求导数
。求导数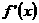 ;(2)若
;(2)若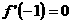 ,求
,求 在区间
在区间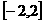 上的最大值和最小值。
上的最大值和最小值。
解析:(1)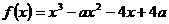 ,
,
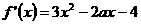 。
。
(2)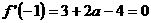 ,
,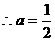 。
。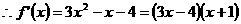
令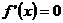 ,即
,即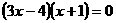 ,解得
,解得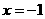 或
或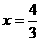 , 则
, 则 和
和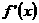 在区间
在区间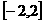 上随
上随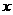 的变化情况如下表:
的变化情况如下表:
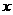 |
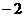 |
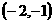 |
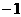 |
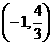 |
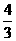 |
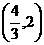 |
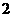 |
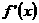 |
|
+ |
0 |
- |
0 |
+ |
|
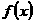 |
0 |
增函数 |
极大值 |
减函数 |
极小值 |
增函数 |
0 |
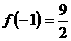 ,
,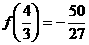 。所以,
。所以, 在区间
在区间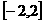 上的最大值为
上的最大值为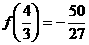 ,最小值为
,最小值为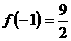 。
。
答案:(1)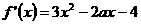 ;(2)最大值为
;(2)最大值为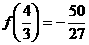 ,最小值为
,最小值为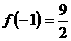 。
。
点评:本题考查可导函数最值的求法。求可导函数 在区间
在区间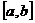 上的最值,要先求出函数
上的最值,要先求出函数 在区间
在区间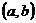 上的极值,然后与
上的极值,然后与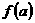 和
和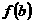 进行比较,从而得出函数的最大最小值。
进行比较,从而得出函数的最大最小值。
考点七:导数的综合性问题。
例8. 设函数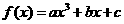
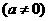 为奇函数,其图象在点
为奇函数,其图象在点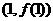 处的切线与直线
处的切线与直线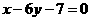 垂直,导函数
垂直,导函数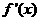 的最小值为
的最小值为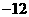 。(1)求
。(1)求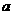 ,
,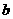 ,
,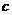 的值;
的值;
(2)求函数 的单调递增区间,并求函数
的单调递增区间,并求函数 在
在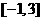 上的最大值和最小值。
上的最大值和最小值。
解析: (1)∵ 为奇函数,∴
为奇函数,∴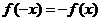 ,即
,即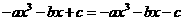
∴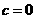 ,∵
,∵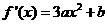 的最小值为
的最小值为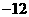 ,∴
,∴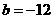 ,又直线
,又直线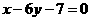 的斜率为
的斜率为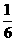 ,因此,
,因此,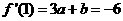 ,∴
,∴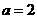 ,
,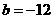 ,
,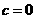 .
.
(2)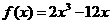 。
。 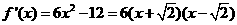 ,列表如下:
,列表如下:
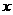 |
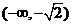 |
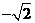 |
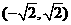 |
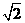 |
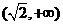 |
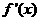 |
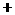 |
 |
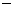 |
 |
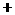 |
 |
增函数 |
极大 |
减函数 |
极小 |
增函数 |
所以函数 的单调增区间是
的单调增区间是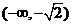 和
和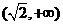 ,∵
,∵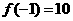 ,
,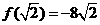 ,
,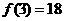 ,∴
,∴ 在
在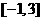 上的最大值是
上的最大值是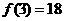 ,最小值是
,最小值是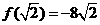 。
。
答案:(1)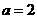 ,
,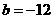 ,
,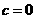 ;(2)最大值是
;(2)最大值是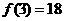 ,最小值是
,最小值是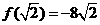 。
。
点评:本题考查函数的奇偶性、单调性、二次函数的最值、导数的应用等基础知识,以及推理能力和运算能力。
3 方法总结与2008年高考预测
3.应用导数解决实际问题,关键是建立恰当的数学模型(函数关系),如果函数在给定区间内只有一个极值点,此时函数在这点有极大(小)值,而此时不用和端点值进行比较,也可以得知这就是最大(小)值。
2.导数的应用是高中数学中的重点内容,导数已由解决问题的工具上升到解决问题必不可少的工具,特别是利用导数来解决函数的单调性与最值问题是高考热点问题。选择填空题侧重于利用导数确定函数的单调性、单调区间和最值问题,解答题侧重于导数的综合应用,即与函数、不等式、数列的综合应用。
1.导数的概念及其运算是导数应用的基础,是高考重点考查的内容。考查方式以客观题为主,主要考查导数的基本公式和运算法则,以及导数的几何意义。
12.设椭圆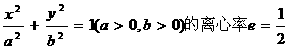 ,右焦点F(c,0),方程
,右焦点F(c,0),方程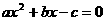 的两个根分别为x1,x2,则点P(x1,x2)在( )
的两个根分别为x1,x2,则点P(x1,x2)在( )
A.圆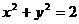 内 B.圆
内 B.圆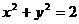 上
上
C.圆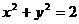 外 D.以上三种情况都有可能
外 D.以上三种情况都有可能
11.an=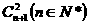 ,则
,则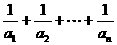 等于( )
等于( )
A.2 B.
B.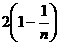 C.2-
C.2- D.1-
D.1-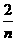
9.在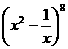 的展开式中,含x的项的系数是( )
的展开式中,含x的项的系数是( )
A.55 B.-55 C.56 D.-56
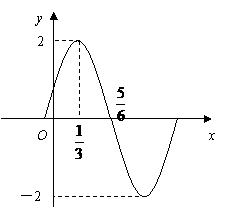
|
 的图象(部分)如图所示,则
的图象(部分)如图所示,则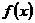 的解析式是( )
的解析式是( )
A.
B.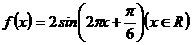
C.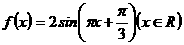
D.
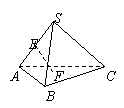
8.如图,在正四面体S-ABC中,E为SA的中点,F为DABC
的中心,则异面直线EF与AB所成的角是( )
A.30° B.45° C.60° D.90°
7.已知定义域为R的函数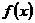 在区间
在区间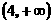 上为减函数,且函数
上为减函数,且函数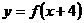 为偶函数,则( )
为偶函数,则( )
 A.
A.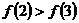 B.
B.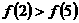 C.
C.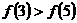 D.
D.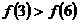
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com