
题目列表(包括答案和解析)
2.用反证法证明命题:若P则q ,其第一步是反设命题的结论不成立,这个命题正确的反设是( )
A.若P则非q B.若非P则q C.非P D.非q
1.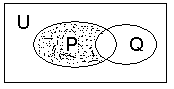 右图中阴影部分表示的集合是( )
右图中阴影部分表示的集合是( )
A.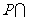
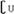
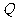 B.
B.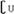
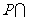
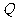
C.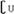 (
(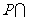
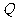 ) D.
) D.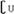 (
(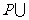
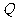 )
)
22.(本小题满分12分)
已知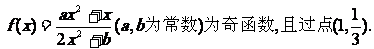
(Ⅰ)求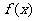 的表达式;
的表达式;
(Ⅱ)定义正数数列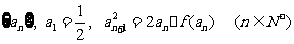 ,证明:数列
,证明:数列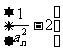 是等比数列;
是等比数列;
|
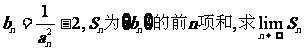 。
。
(文) 令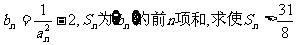 成立的最小n值。
成立的最小n值。
21.(本小题满分12分)
两个二次函数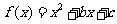 与
与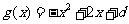 的图像有唯一的公共点
的图像有唯一的公共点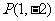 ,
,
(Ⅰ)求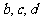 的值;
的值;
(Ⅱ)(理)设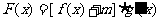 ,若
,若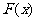 在
在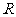 上是单调函数,求
上是单调函数,求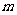 的范围。并说明函数是R上的单调递增函数还是单调递减函数。
的范围。并说明函数是R上的单调递增函数还是单调递减函数。
(文)设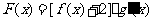 ,求
,求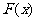 在x∈[-1,2]上的最大值和最小值。
在x∈[-1,2]上的最大值和最小值。
20.(本小题满分12分)
如图,设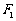 、
、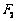 分别为椭圆
分别为椭圆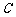 :
: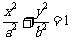 (
(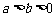 )的左、右焦点.设椭圆C上的点
)的左、右焦点.设椭圆C上的点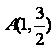 到F1、F2两点距离之和等于4。
到F1、F2两点距离之和等于4。
(Ⅰ)求椭圆C的方程和离心率;
(Ⅱ)若P(x,y)是该椭圆上的一个动点,求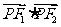 的最大值和最小值。
的最大值和最小值。

19.(本小题满分12分)
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2, PA=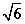

(Ⅰ)求证:PA⊥B1D1;
(Ⅱ)求平面PAD与平面BDD1B1所成的锐二面角θ的大小;
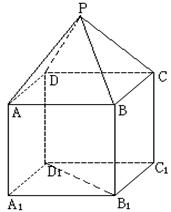 (Ⅲ)求B1到平面PAD的距离。
(Ⅲ)求B1到平面PAD的距离。
18.(本小题满分12分)
在锐角ABC中,设a、b、c分别为角A、B、C的对边,S为ABC的面积,且满足条件: 2sinB [
1+cos(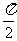 -B)] +cos2B=1+.
-B)] +cos2B=1+.
(Ⅰ)求B的度数;
(Ⅱ)若a=4,S=5,求c和b的值。
17.(本小题满分10分)
乌鲁木齐市高级中学的成功同学到甲、乙、丙三所高校参加自主招生考试,各高校是否录取他相互独立。成功同学被甲、乙、丙三所高校录取的概率分别为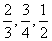 。(假设允许成功同学可以被多所高校同时录取)
。(假设允许成功同学可以被多所高校同时录取)
(Ⅰ)求成功同学没有被录取的概率;
(Ⅱ)(理)求录取成功同学的高校数ξ的分布列和数学期望。
(文)成功同学被几个高校同时录取的可能性最大?
16.(理)设函数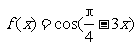 ,则
,则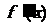 是
是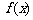 的导数,则
的导数,则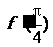 =_______。
=_______。
(文)已知正方体的表面积为18,则正方体的外接球的体积等于 。
15.若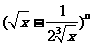 的展开式的第四项是常数项,则为
的展开式的第四项是常数项,则为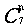 =
。
=
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com