
题目列表(包括答案和解析)
4.若点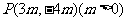 在角
在角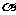 的终边上,则
的终边上,则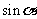 的值是( )
的值是( )
A、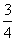 B、
B、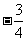 C、
C、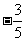 D、
D、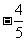
3.已知全集U=R,设函数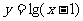 的定义域为集合A,函数
的定义域为集合A,函数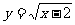 的定义域为集合B,则
的定义域为集合B,则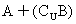 = (
)
= (
)
A.[1,2] B.[1,2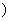 C.
C.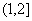 D.(1,2)
D.(1,2)
2. “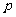 或
或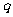 是假命题”是“非
是假命题”是“非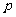 为真命题”的
( )
为真命题”的
( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
1.若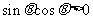 ,则
,则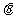 在( )
在( )
A.第一象限 B.第一、二象限 C.第一、三象限 D.第二、四象限
21.过曲线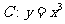 上的点
上的点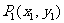 作曲线
作曲线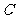 的切线l1与曲线
的切线l1与曲线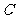 交于点
交于点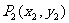 ,过点
,过点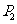 作曲线
作曲线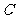 的切线l2与曲线
的切线l2与曲线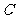 交于点
交于点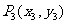 ,依此类推,可得到点列:
,依此类推,可得到点列: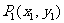 ,
,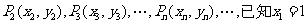 .
.
(1)求点P2、P3的坐标;
(2)求数列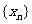 的通项公式;
的通项公式;
(3)记点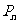 到直线
到直线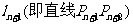 的距离为
的距离为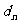 ,
,
求证: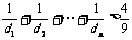 .
.
20.(本小题满分14分)
已知函数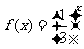 .
.
(1) 若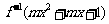 的定义域为
的定义域为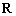 ,求实数
,求实数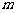 的取值范围;
的取值范围;
(2) 当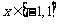 时,求函数
时,求函数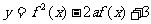 的最小值
的最小值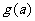 .
.
(3) 是否存在实数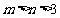 ,使得
,使得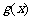 的定义域为
的定义域为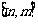 ,值域为
,值域为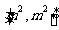 ,若存在,求出
,若存在,求出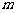 、
、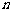 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
19.(本大题满分14分)如图,在五面体ABCDEF中,四边形ABCD为矩形,对角线AC,BD的交点为O,△ABF和△DEC为等边三角形,棱EF∥BC,EF= BC,AB=1,BC=2,M为EF的中点,
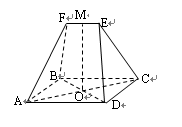 ①求证:OM⊥平面ABCD;
①求证:OM⊥平面ABCD;
②求二面角E-CD-A的大小;
③求点A到平面CDE的距离。
18.(本小题满分14分)
已知直线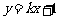 与双曲线
与双曲线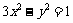 有A、B两个不同的交点.
有A、B两个不同的交点.
(1)如果以AB为直径的圆恰好过原点O,试求k的值;
(2)是否存在k,使得两个不同的交点A、B关于直线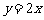 对称?试述理由.
对称?试述理由.
17.(本小题满分12分)
已知向量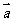 =(
=(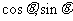 ),
), 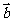 =(
=(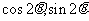 ),
),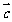 =(-1,0),
=(-1,0), 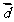 =(0,1).
=(0,1).
(1)求证: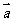 ⊥(
⊥(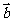 +
+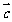 )
) 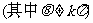 ;
;
(2)设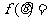
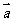 ·(
·(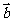 -
-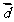 ),且
),且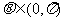 ,求
,求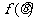 的值域.
的值域.
16.非空集合M关于运算 满足:(1)对任意的a,
满足:(1)对任意的a,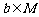 ,都有
,都有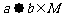 ;(2)存在
;(2)存在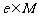 ,使得对一切
,使得对一切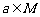 ,都有
,都有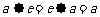 ,则称M关于运算
,则称M关于运算 为“理想集”.
为“理想集”.
现给出下列集合与运算:
①M={非负整数}, 为整数的加法;②M={偶数},
为整数的加法;②M={偶数}, 为整数的乘法;
为整数的乘法;
③M={二次三项式}, 为多项式的加法;④M={平面向量},
为多项式的加法;④M={平面向量}, 为平面向量的加法;
为平面向量的加法;
其中M关于运算 为“理想集”的是
.(只需填出相应的序号)
为“理想集”的是
.(只需填出相应的序号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com