
题目列表(包括答案和解析)
3.设等差数列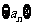 的前n项和为
的前n项和为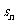 。若
。若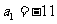 ,
,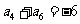 ,则当
,则当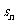 取最小值时,n等于
取最小值时,n等于
A.6 B.7 C.8 D.9
2.以抛物线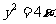 的焦点为圆心,且过坐标原点的圆的方程为
的焦点为圆心,且过坐标原点的圆的方程为
A.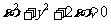 B.
B.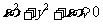
 C.
C.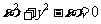 D.
D.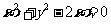
1.计算sin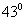 cos
cos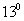 -cos
-cos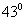 sin
sin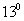 的结果等于
的结果等于
A.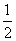 B.
B. 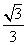 C.
C.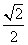 D.
D.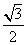
(16)(本小题满分13分,(I)小问7分,(II)小问6分)
设函数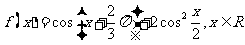 。
。
(I)
求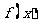 的值域;
的值域;
(II)
记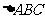 的内角A、B、C的对边长分别为a,b,c,若
的内角A、B、C的对边长分别为a,b,c,若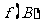 =1,b=1,c=
=1,b=1,c=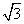 ,求a的值。
,求a的值。
(17)(本小题满分13分,(I)小问5分,(II)小问8分)
在甲、乙等6个单位参加的一次“唱读讲传”演出活动中,每个单位的节目集中安排在一起,若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,……6),求:
(I)甲、乙两单位的演出序号至少有一个为奇数的概率;
(II)甲、乙两单位之间的演出单位个数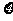 的分布列与期望。
的分布列与期望。
(18)(本小题满分13分,(I)小问5分,(II)小问8分)
已知函数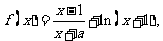 其中实数
其中实数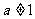 。
。
(I)
若a=-2,求曲线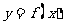 在点
在点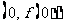 处的切线方程;
处的切线方程;
(II)
若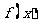 在x=1处取得极值,试讨论
在x=1处取得极值,试讨论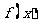 的单调性。
的单调性。
(19)(本小题满分12分,(I)小问5分,(II)小问7分)
如题(19)图,四棱锥P-ABCD中,底面ABCD为矩形,PA 底面ABCD,PA=AB=
底面ABCD,PA=AB=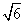 ,点E是棱PB的中点。
,点E是棱PB的中点。
(I) 求直线AD与平面PBC的距离;
(II)
若AD=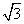 ,求二面角A-EC-D的平面角的余弦值。
,求二面角A-EC-D的平面角的余弦值。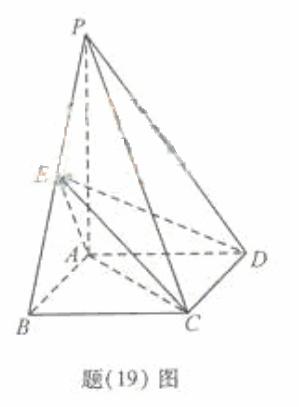
(20)(本小题满分12分,(I)小问5分,(II)小问7分)
已知以原点O为中心,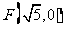 为右焦点的双曲线C的离心率
为右焦点的双曲线C的离心率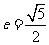 。
。
(I) 求双曲线C的标准方程及其渐近线方程;
(II)
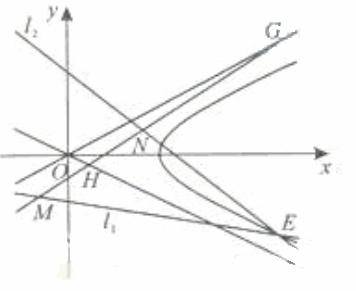
如题(20)图,已知过点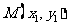 的直线
的直线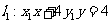 与过点
与过点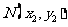 (其中
(其中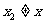 )的直线
)的直线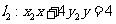 的交点E在双曲线C上,直线MN与两条渐近线分别交与G、H两点,求
的交点E在双曲线C上,直线MN与两条渐近线分别交与G、H两点,求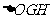 的面积。
的面积。
(21)(本小题满分12分,(I)小问5分,(II)小问7分)
在数列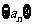 中,
中,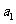 =1,
=1,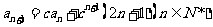 ,其中实数
,其中实数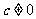 。
。
(I)
求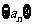 的通项公式;
的通项公式;
(II)
若对一切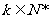 有
有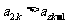 ,求c的取值范围。
,求c的取值范围。
(11)已知复数z=1+I ,则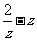 =____________.
=____________.
(12)设U=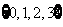 ,A=
,A=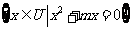 ,若
,若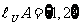 ,则实数m=_________.
,则实数m=_________.
(13)某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至多命中一次的概率为
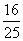 ,则该队员每次罚球的命中率为____________.
,则该队员每次罚球的命中率为____________.
(14)已知以F为焦点的抛物线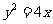 上的两点A、B满足
上的两点A、B满足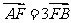 ,则弦AB的中点到准线的距离为___________.
,则弦AB的中点到准线的距离为___________.
(15)已知函数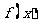 满足:
满足: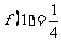 ,
,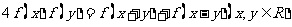 ,则
,则 =_____________.
=_____________.
(1)在等比数列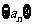 中,
中,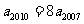 ,则公比q的值为
,则公比q的值为
A. 2 B. 3 C. 4 D. 8
(2) 已知向量a,b满足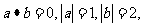 ,则
,则
A. 0
B. 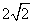 C. 4 D. 8
C. 4 D. 8
(3)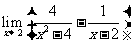 =
=
A. -1
B. -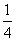 C.
C. 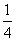 D. 1
D. 1
(4)设变量x,y满足约束条件 ,则z=2x+y的最大值为
,则z=2x+y的最大值为
A.-2 B. 4 C. 6 D. 8
(5) 函数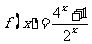 的图象
的图象
A. 关于原点对称 B. 关于直线y=x对称 C. 关于x轴对称 D. 关于y轴对称
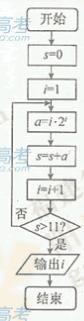
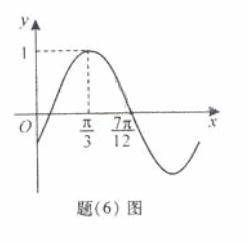
(6)已知函数 的部分图象如题(6)图所示,则
的部分图象如题(6)图所示,则
A.
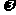 =1
=1 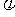 =
= 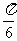 B.
B. 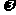 =1
=1 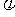 =-
=- 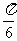 C.
C. 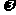 =2
=2 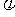 =
= 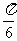 D.
D. 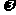 =2
=2 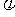 = -
= -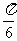
(7)已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值是
A. 3 B. 4 C. 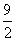 D.
D.
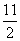
(8) 直线y=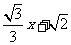 与圆心为D的圆
与圆心为D的圆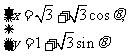
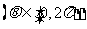 交与A、B两点,则直线AD与BD的倾斜角之和为
交与A、B两点,则直线AD与BD的倾斜角之和为
A. 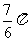 B.
B. 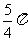 C.
C. 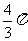 D.
D.
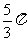
(9)某单位安排7位员工在10月1日至7日值班,每天1人,每人值班1天,若7位员工中的甲、乙排在相邻两天,丙部排在10月1日,也不排在10月7日,则不同的安排方案共有
A. 504种 B. 960种 C. 1008种 D. 1108种
(10)到两互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是
A. 直线 B. 椭圆 C. 抛物线 D. 双曲线
(17)(本小题满分12分)
某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为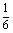 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(Ⅰ)求甲中奖且乙、丙都没有中奖的概率;
(Ⅱ)求中奖人数ξ的分布列及数学期望Eξ.
(18)(本小题满分12分)
已知正方体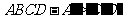 的棱长为1,点
的棱长为1,点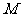 是棱
是棱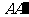 的中点,点
的中点,点 是对角线
是对角线 的中点.
的中点.
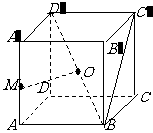 (Ⅰ)求证:
(Ⅰ)求证: 为异面直线
为异面直线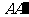 和
和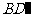 的公垂线;
的公垂线;
(Ⅱ)求二面角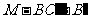 的大小;
的大小;
(Ⅲ)求三棱锥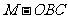 的体积.
的体积.
(19)(本小题满分12分)
(Ⅰ)1证明两角和的余弦公式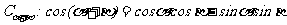 ;
;
2由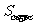 推导两角和的正弦公式
推导两角和的正弦公式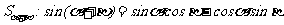 .
.
(Ⅱ)已知△ABC的面积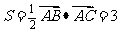 ,且
,且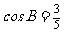 ,求
,求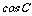 .
.
(20)(本小题满分12分)
已知定点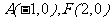 ,定直线
,定直线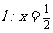 ,不在
,不在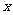 轴上的动点
轴上的动点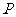 与点
与点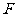 的距离是它到直线
的距离是它到直线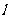 的距离的2倍.设点
的距离的2倍.设点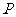 的轨迹为
的轨迹为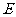 ,过点
,过点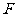 的直线交
的直线交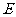 于
于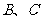 两点,直线
两点,直线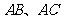 分别交
分别交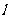 于点
于点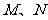
(Ⅰ)求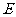 的方程;
的方程;
(Ⅱ)试判断以线段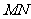 为直径的圆是否过点
为直径的圆是否过点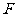 ,并说明理由.
,并说明理由.
(21)(本小题满分12分)
已知数列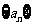 满足
满足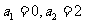 ,且对任意
,且对任意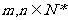 都有
都有
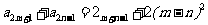
(Ⅰ)求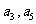 ;
;
(Ⅱ)设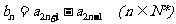 证明:
证明: 是等差数列;
是等差数列;
(Ⅲ)设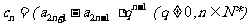 ,求数列
,求数列 的前
的前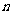 项和
项和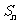 .
.
(22)(本小题满分14分)
设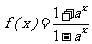 (
(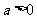 且
且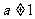 ),
),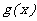 是
是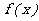 的反函数.
的反函数.
(Ⅰ)设关于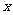 的方程求
的方程求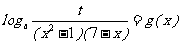 在区间
在区间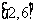 上有实数解,求
上有实数解,求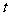 的取值范围;
的取值范围;
(Ⅱ)当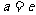 (
(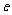 为自然对数的底数)时,证明:
为自然对数的底数)时,证明: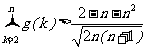 ;
;
(Ⅲ)当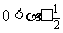 时,试比较
时,试比较 与4的大小,并说明理由.
与4的大小,并说明理由.
(13)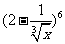 的展开式中的第四项是
.
的展开式中的第四项是
.
(14)直线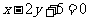 与圆
与圆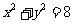 相交于A、B两点,则
相交于A、B两点,则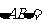 .
.
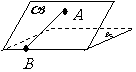 (15)如图,二面角
(15)如图,二面角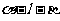 的大小是60°,线段
的大小是60°,线段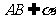 .
.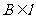 ,
,
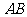 与
与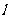 所成的角为30°.则
所成的角为30°.则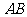 与平面
与平面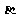 所成的角的正弦值是
.
所成的角的正弦值是
.
(16)设S为复数集C的非空子集.若对任意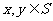 ,都有
,都有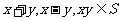 ,则称S为封闭集。下列命题:
,则称S为封闭集。下列命题:
1集合 (
(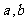 为整数,
为整数,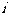 为虚数单位)为封闭集;
为虚数单位)为封闭集;
2若S为封闭集,则一定有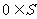 ;
;
3封闭集一定是无限集;
4若S为封闭集,则满足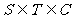 的任意集合
的任意集合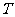 也是封闭集.
也是封闭集.
其中真命题是 (写出所有真命题的序号)
(1)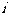 是虚数单位,计算
是虚数单位,计算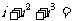
(A)-1 (B)1
(C) (D)
(D)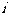
(2)下列四个图像所表示的函数,在点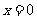 处连续的是
处连续的是
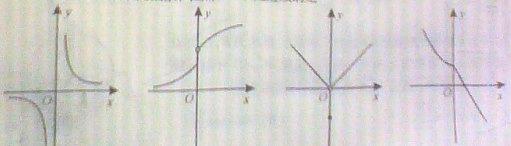
(A) (B) (C) (D)
(3)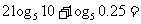
(A)0 (B)1 (C) 2 (D)4
(4)函数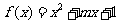 的图像关于直线
的图像关于直线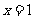 对称的充要条件是
对称的充要条件是
(A)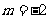 (B)
(B)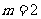 (C)
(C)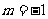 (D)
(D)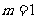
(5)设点M是线段BC的中点,点A在直线BC外,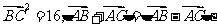 则
则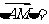
(A)8 (B)4 (C) 2 (D)1
(6)将函数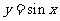 的图像上所有的点向右平行移动
的图像上所有的点向右平行移动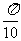 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是
(A)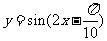 (B)
(B)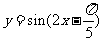
(C)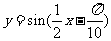 (D)
(D)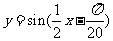
(7)某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元,乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙两车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为
(A)甲车间加工原料10箱,乙车间加工原料60箱
(B)甲车间加工原料15箱,乙车间加工原料55箱
(C)甲车间加工原料18箱,乙车间加工原料50箱
(D)甲车间加工原料40箱,乙车间加工原料30箱
(8)已知数列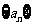 的首项
的首项 ,其前
,其前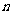 项的和为
项的和为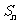 ,且
,且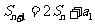 ,则
,则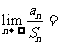
(A)0 (B)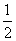 (C) 1
(D)2
(C) 1
(D)2
(9)椭圆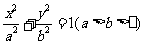 的右焦点
的右焦点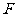 ,其右准线与
,其右准线与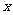 轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点
轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点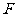 ,则椭圆离心率的取值范围是
,则椭圆离心率的取值范围是
(A)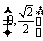 (B)
(B)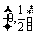 (C)
(C)
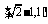 (D)
(D)
(10)由1、2、3、4、5、6组成没有重复数字且1、3都不与5相邻的六位偶数的个数是
 (A)72 (B)96
(C) 108
(D)144
(A)72 (B)96
(C) 108
(D)144
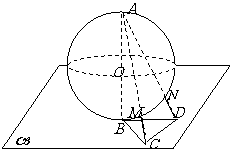
(11)半径为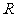 的球
的球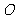 的直径
的直径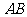 垂直于平面
垂直于平面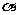 ,垂足为
,垂足为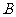 ,
,
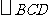 是平面
是平面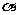 内边长为
内边长为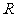 的正三角形,线段
的正三角形,线段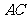 、
、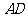 分别
分别
与球面交于点M,N,那么M、N两点间的球面距离是
(A)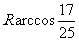 (B)
(B)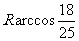
(C)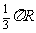 (D)
(D)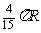
(12)设 ,则
,则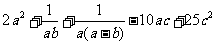 的最小值是
的最小值是
(A)2 (B)4 (C) 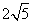 (D)5
(D)5
第Ⅱ卷
(17)(本小题满分10分)
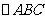 中,
中,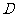 为边
为边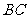 上的一点,
上的一点,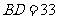 ,
,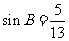 ,
,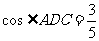 ,求
,求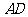 。
。
(18)(本小题满分12分)
已知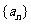 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且
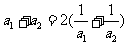 ,
,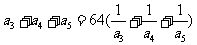
(Ⅰ)求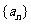 的通项公式;
的通项公式;
(Ⅱ)设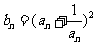 ,求数列
,求数列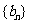 的前
的前 项和
项和 。
。
(19)(本小题满分12分)
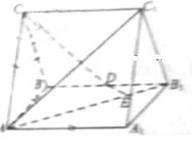 如图,直三棱柱ABC-A
如图,直三棱柱ABC-A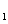 B
B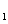 C
C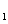 中,AC=BC, AA
中,AC=BC, AA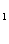 =AB,D为BB
=AB,D为BB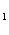 的中点,E为AB
的中点,E为AB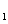 上的一点,AE=3 EB
上的一点,AE=3 EB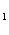
(Ⅰ)证明:DE为异面直线AB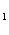 与CD的公垂线;
与CD的公垂线;
(Ⅱ)设异面直线AB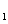 与CD的夹角为45°,求二面角A
与CD的夹角为45°,求二面角A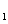 -AC
-AC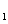 -B
-B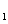 的大小
的大小
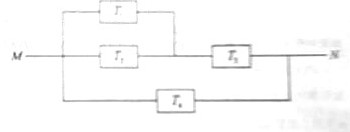
(20)(本小题满分12分)
如图,由M到N的电路中有4个元件,分别标为T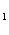 ,T
,T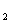 ,T
,T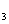 ,T
,T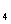 ,电源能通过T
,电源能通过T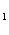 ,T
,T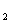 ,T
,T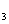 的概率都是P,电源能通过T
的概率都是P,电源能通过T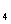 的概率是0.9,电源能否通过各元件相互独立。已知T
的概率是0.9,电源能否通过各元件相互独立。已知T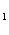 ,T
,T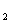 ,T
,T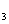 中至少有一个能通过电流的概率为0.999。
中至少有一个能通过电流的概率为0.999。
(Ⅰ)求P;
(Ⅱ)求电流能在M与N之间通过的概率。
(21)(本小题满分12分)
已知函数f(x)=x -3ax
-3ax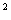 +3x+1。
+3x+1。
(Ⅰ)设a=2,求f(x)的单调期间;
(Ⅱ)设f(x)在区间(2,3)中至少有一个极值点,求a的取值范围。
(22)(本小题满分12分)
已知斜率为1的直线1与双曲线C: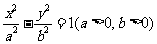 相交于B、D两点,且BD的中点为M(1.3)
相交于B、D两点,且BD的中点为M(1.3)
(Ⅰ)(Ⅰ)求C的离心率;
(Ⅱ)(Ⅱ)设C的右顶点为A,右焦点为F,|DF|·|BF|=17证明:过A、B、D三点的圆与x轴相切。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com