5. 在二项式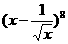的展开式中，含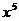的项的系数是　　　　　　　 (用数字作答).

4. 计算：　　　　　 .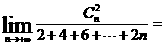

3．经过抛物线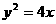的焦点，且以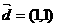为方向向量的直线的方程是　　　　　 .

2．若函数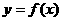与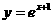的图像关于直线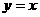对称，则　　　　　 　　.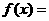

1. 不等式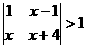的解集是___________.

23．(本题满分18分)本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分．

对于定义域为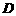的函数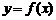，若有常数M，使得对任意的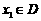，存在唯一的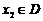满足等式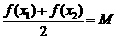，则称M为函数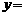f (x)的“均值”．

(1)判断1是否为函数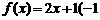≤≤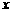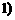的“均值”，请说明理由；

(2)若函数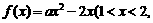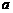为常数)存在“均值”，求实数a的取值范围；

(3)若函数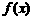是单调函数，且其值域为区间I．试探究函数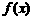的“均值”情况(是否存在、个数、大小等)与区间I之间的关系，写出你的结论(不必证明)．

说明：对于(3)，将根据结论的完整性与一般性程度给予不同的评分

22．(本题满分18分)本题共有3个小题，第1小题满分4分，第2小题满分5分，第3小题满分9分．

已知数列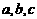是各项均为正数的等差数列，公差为d(d 0)．在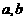之间和b,c之间共插入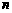个实数，使得这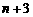个数构成等比数列，其公比为q．

(1)求证：；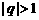

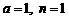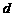(2)若，求的值；

(3)若插入的n个数中，有s个位于a,b之间，t个位于b,c之间，且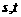都为奇数，试比较s与t的大小，并求插入的n个数的乘积(用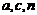表示).

21．(本题满分13分)本题共有2个小题，第1小题满分6分，第2小题满分7分．

已知椭圆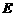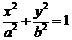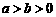：()过点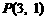，其左、右焦点分别为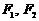，且

．

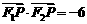(1)求椭圆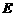的方程；

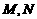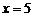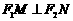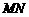(2)若是直线上的两个动点，且，则以为直径的圆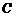是否过定点？请说明理由．

20．(本题满分13分)本题共有2个小题，第1小题满分5分，第2小题满分8分．

某校10名学生组成该校“科技创新周”志愿服务队(简称“科服队”)，他们参加活动的有关数据统计如下：

(1)从“科服队”中任选3人，求这3人参加活动次数各不相同的概率；

(2)从“科服队”中任选2人，用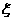表示这2人参加活动次数之差的绝对值，求随机变量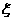的分布列及数学期望．

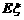19．(本题满分12分)

已知矩形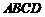内接于圆柱下底面的圆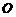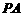，是圆柱的母线，若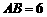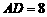，，此圆柱的体积为，求异面直线与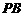所成角的余弦值．