
题目列表(包括答案和解析)
18. (本题满分14分)
如图(1), 是等腰直角三角形,
是等腰直角三角形,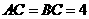 ,
,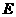 、
、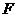 分别为
分别为 、
、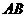 的中点,将
的中点,将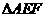 沿
沿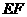 折起,使
折起,使 在平面
在平面 上的射影
上的射影 恰为
恰为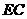 的中点,得到图(2).
的中点,得到图(2).
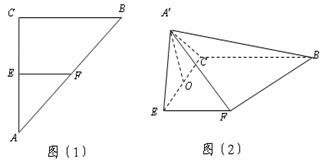 (1)求证:
(1)求证: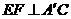 ; (2)求三棱锥
; (2)求三棱锥 的体积.
的体积.
17.(本题满分12分)
为预防 病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
|
|
A组 |
B组 |
C组 |
|
疫苗有效 |
673 |
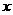 |
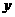 |
|
疫苗无效 |
77 |
90 |
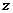 |
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(1)求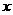 的值;
的值;
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取多少个?
(3)已知y 465,z
465,z 25,求不能通过测试的概率.
25,求不能通过测试的概率.
16.(本小题满分12分)
已知函数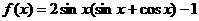 .
.
(1)求函数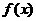 的最小正周期和最大值;
的最小正周期和最大值;
(2)在给定的坐标系内,用五点作图法画
出函数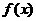 在一个周期内的图象.
在一个周期内的图象.
(二)选做题,14、15两题任选一个,做对记5分,两题都做以第一题记分
14. 若直线
若直线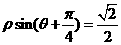 与直线
与直线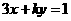 垂直,则常数
垂直,则常数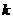 = .
= .
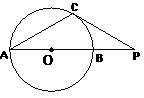
15.如图,AB是⊙O的直径,延长AB到点P,使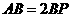 ,过
,过
点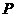 作⊙O的切线,切点为
作⊙O的切线,切点为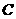 ,连接
,连接 , 则
, 则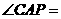 __ _.
__ _.
(一)必做题(11~13题)
11.已知平面向量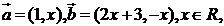
若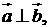 则实数
则实数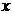 的值是 ;
的值是 ;
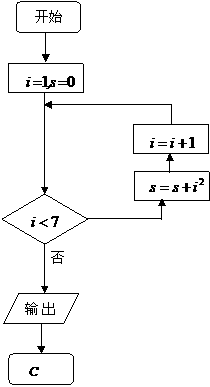
12.利用如图算法在平面直角坐标系上打印一系列点,
则打印的点能落在不等式组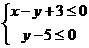
所表示的区域内的点有 个.
13. 已知总体的各个体的值由小到大依次为2,3,3,7,a,b,12,13.7,18.3,20,且总体的中位数为10.5.若要使该总体的方差最小,则a、b的取值分别是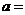 ,
,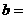 _______ ;
_______ ;
10. 定义域为R的函数
定义域为R的函数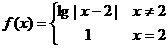 ,若关于
,若关于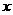 的方程
的方程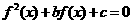 恰有3个不同的实数解
恰有3个不同的实数解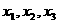 ,则
,则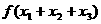 等于( )
等于( )
A.0 B.l C.3lg2 D.2lg2
9.过双曲线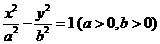 的右顶点
的右顶点 作斜率为
作斜率为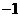 的直线,该直线与双曲线的两条渐近线的交点分别为
的直线,该直线与双曲线的两条渐近线的交点分别为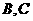 .若
.若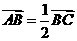 ,则双曲线的离心率是 (
)
,则双曲线的离心率是 (
)
A.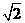 B.
B.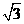 C.
C.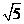 D.
D.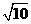
8. 已知平面上不重合的四点P,A,B,C满足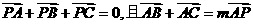 ,那么实数m的值为( )
,那么实数m的值为( )
A.2 B.3 C.4 D.5
7.给出四个命题:
①平行于同一平面的两个不重合的平面平行; ②平行于同一直线的两个不重合的平面平行;
③垂直于同一平面的两个不重合的平面平行; ④垂直于同一直线的两个不重合的平面平行;
其中真命题的个数是( )
A.1 B.2 C.3 D.4
6.已知变量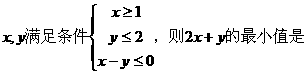 ( )
( )
A. 6 B. 4 C. 3 D. 2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com