
题目列表(包括答案和解析)
21.已知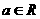 ,函数
,函数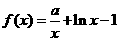 ,
,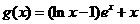 .
.
(1)求函数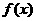 在区间
在区间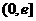 上的最小值;
上的最小值;
(2)是否存在实数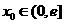 ,使曲线
,使曲线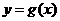 在点
在点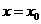 处的切线与
处的切线与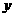 轴垂直?若存在,求出
轴垂直?若存在,求出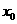 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)求证: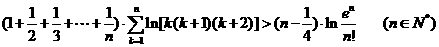 .
.
20.已知椭圆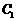 和抛物线
和抛物线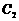 有公共焦点F(1,0),
有公共焦点F(1,0),
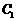 的中心和
的中心和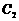 的顶点都在坐标原点,过点M(4,0)的直线
的顶点都在坐标原点,过点M(4,0)的直线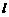 与抛物线
与抛物线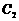 分别相交于A,B两点.
分别相交于A,B两点.
(1)写出抛物线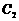 的标准方程;
的标准方程;
(2)若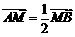 ,求直线
,求直线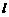 的方程;
的方程;
(3)若坐标原点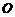 关于直线
关于直线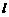 的对称点
的对称点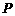 在抛物线
在抛物线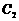 上,直线
上,直线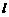 与椭圆
与椭圆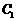 有公共点,求椭圆
有公共点,求椭圆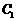 的长轴长的最小值.
的长轴长的最小值.
19.设数列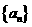 的前n项积为
的前n项积为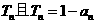 ;数列
;数列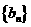 的前n项和为
的前n项和为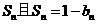 .
.
(1)设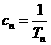 .①证明数列
.①证明数列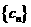 成等差数列;②求证数列
成等差数列;②求证数列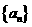 的通项公式;
的通项公式;
(2)若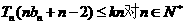 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
18.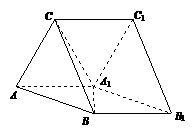 已知三棱柱
已知三棱柱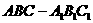 ,侧面
,侧面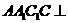 侧面
侧面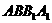 ,
,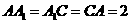 ,
,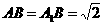 。
(1)求证:
。
(1)求证: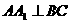 ;
(2)求二面角
;
(2)求二面角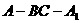 的余弦值;
(3)若
的余弦值;
(3)若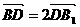 ,在线段
,在线段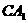 上是否存在一点
上是否存在一点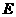 ,使得
,使得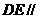 平
平
面 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
.
17.一个口袋中装有大小相同的2个白球和4个黑球.
(1)采取放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(2)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的期望和方差.
16.已知函数 的图象与直线
的图象与直线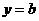
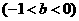 的三个相邻交点的横坐标分别是
的三个相邻交点的横坐标分别是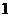 ,
,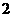 ,
,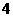 .
(1)求
.
(1)求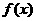 的解析式,并写出
的解析式,并写出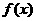 的单调递减区间;
(2)设
的单调递减区间;
(2)设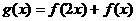 ,求函数
,求函数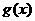 的值域
的值域
15.(在下列两题中任选一题,若两题都做,按第1题给分)
①若曲线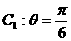
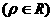 与曲线
与曲线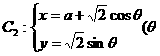 为参数,
为参数,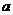 为常数,
为常数,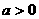 )有两个交点A、B,且|AB|=2,则实数
)有两个交点A、B,且|AB|=2,则实数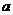 的值为 。
的值为 。
②已知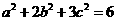 ,若存在实数
,若存在实数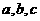 ,使得不等式
,使得不等式 成立,则实数
成立,则实数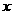 的取值范围为___ _
的取值范围为___ _
14.如图所示,将数以斜线作如下分群:(1),(2,3),(4,6,5),
(8,12,10,7),(16,24,20,14,9),…。并顺次称其为第1群,第2群,
第3群,第4群,….则第7群中的第2项是: ;
|
1 |
3 |
5 |
7 |
9 |
… |
|
2 |
6 |
10 |
14 |
18 |
… |
|
4 |
12 |
20 |
28 |
36 |
… |
|
8 |
24 |
40 |
56 |
72 |
… |
|
16 |
48 |
80 |
112 |
114 |
… |
|
… |
… |
… |
… |
… |
… |
第n群中n个数的和是: 。
13.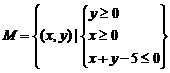 ,
,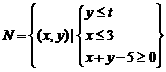 ,
,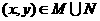 ,
,
当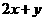 取得最大值时,
取得最大值时,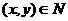 ,
,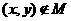 ,则实数
,则实数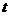 的取值范围是 .
的取值范围是 .
12.已知点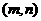 在直线
在直线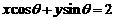 上,则
上,则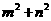 的最小值为 .
的最小值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com