
题目列表(包括答案和解析)
20.(本小题满分12分)
(理)某植物研究所进行种子的发芽实验,已知某种植物种子每粒成功发芽的概率都为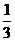 ,每次实验种一粒种子, 每次实验结果相互独立. 假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验, 设
,每次实验种一粒种子, 每次实验结果相互独立. 假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该研究所共进行四次实验, 设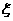 表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.
表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.
(1)求随机变量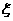 的分布列及
的分布列及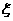 的数学期望
的数学期望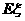 ;
;
(2)记“不等式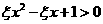 的解集是实数集
的解集是实数集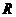 ”为事件
”为事件 ,求事件
,求事件 发生的概率
发生的概率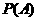 .
.
(文)为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18] .按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.
(1)将频率当作概率,求调查中随机抽取了多少个学生的百米成绩;
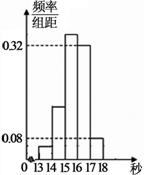 (2)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.
(2)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.
19.(本小题满分12分)
(理)已知函数f(x)=+-1(a∈R)
(1)求函数f(x)的图象在点(1,f(1))处的切线方程;
(2)若f(x)≤0在区间(0,e2]上恒成立,求实数a的取值范围.
(文)已知函数f(x)=x3-3ax,
(1)求函数f(x)的单调区间;
(2)当a=1时,求证:直线4x+y+m=0不可能是函数f(x)图象的切线.
18.(本小题满分12分)
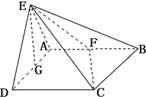 (理)如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°的角.
(理)如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°的角.
(1)求证:EG⊥平面ABCD
(2)当AD=2时,求二面角E-FC-G的大小.
 (文)如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,
(文)如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,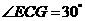
(1)求证:EG⊥平面ABCD
(2)若M,N分别是EB,CD的中点,求证MN//平面EAD.
(3)若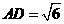 ,求三棱锥
,求三棱锥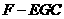 的体积
的体积
17.(本小题满分12分)
(理)已知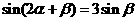 ,设
,设 ,记
,记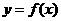
(1)求证:tan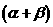 =2tan
=2tan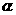
(2)求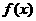 的表达式;
的表达式;
(3)定义正数数列{an}:a1=2,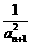 =2
=2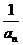
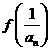 (n
(n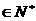 )。试求数列
)。试求数列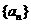 的通项公式。
的通项公式。
(文)已知tan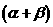 =2tan
=2tan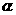 ,设
,设 ,记
,记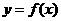
(1)求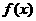 的表达式;
的表达式;
(2)定义正数数列{an}:a1=2,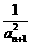 =2
=2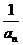
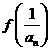 (n
(n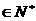 )。试求数列
)。试求数列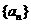 的通项公式。
的通项公式。
16.有一个半径为5的圆,现在将一枚半径为1硬币向圆投去,假设硬币完全落在圆内,则硬币完全落入圆内的概率为 。
15.若当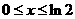 时,不等式
时,不等式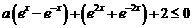 恒成立,则实数
恒成立,则实数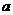 的取值范围是
。
的取值范围是
。
14.在△ABC中,设角A、B、C的对边分别为a,b,c,若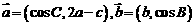 且
且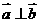 ,则角B=
。
,则角B=
。
13.过椭圆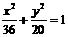 的一个焦点F作弦AB,则
的一个焦点F作弦AB,则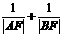 =
。
=
。
12.(理)已知函数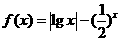 有两个零点
有两个零点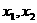 ,则有 ( )
,则有 ( )
A.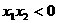 B.
B.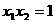 C.
C.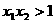 D.
D.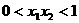
(文)已知函数f(x)=|lgx|.若0<a<b,且f(a)=f(b),则如结论中错误的是 ( )
A.0<a<1 B.b>1 C.ab=1 D.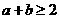
第Ⅱ卷(非选择题 共90分)
11.已知抛物线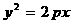
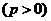 与双曲线
与双曲线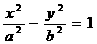
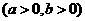 有相同的焦点
有相同的焦点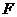 ,点
,点 是两曲线的一个交点,且
是两曲线的一个交点,且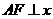 轴,则双曲线的离心率为
( )
轴,则双曲线的离心率为
( )
A.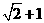 B.
B.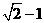 C.
C.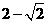 D.
D.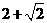
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com