
题目列表(包括答案和解析)
7.设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这五个球放入盒内,要求每盒内放一个球,则恰好有两个球的编号与盒子的编号相同的放法有 ( )
A.20种 B.30种 C.60种 D.120种
6、若C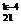 <C
<C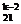 <C
<C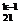 ,(k∈N),则k的取值范围是
( )
,(k∈N),则k的取值范围是
( )
(A)[5,11] (B)[4,13] (C)[4,12] (D)[4,11]
5.3 名男同学,3名女同学站成一排,男女间隔的排法的种数为 ( )
(A)A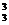 A
A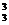 (B)2 A
(B)2 A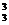 A
A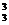 (C)A
(C)A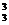 A
A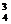 (D)2 A
(D)2 A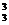 A
A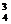
4.四面体的一个顶点为A,从其它顶点与各棱的中点中取3个点,使它们和点A在同一平面上,不同的取法有 ( )
A.30种 B.33种 C.36种 D.39种
3.有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人承担,从10人中选派4人承担这三项任务的不同选法有 ( )
A.1260种 B.2025种 C.2520种 D.5040种
2、有3封信和4 个邮筒, 则将信全部投入邮筒的所有不同的投法种数为 ( )
(A)
A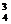 (B) 43 (C)34 (D)
(B) 43 (C)34 (D)
1.某游人上山, 从前山上山的道路有3 条, 从后山上山的道路有2 条, 那么游人从上山到下山, 不同的走法共有 ( )
A.5 种 B.6 种 C.19种 D.25种
11.提示:(1)当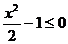 ,即
,即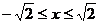 时,
时,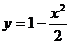 ,由图像可知P(0,a)在这条抛物线顶点A(0,1)的正上方,故|PA|=a-1为最短距离
,由图像可知P(0,a)在这条抛物线顶点A(0,1)的正上方,故|PA|=a-1为最短距离
(2)当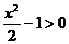 ,即
,即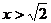 或
或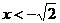 时,
时,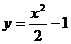 ,设抛物线
,设抛物线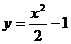 上任意一点
上任意一点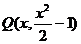 ,则
,则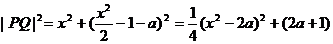
∵2a>2 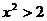 ,则
,则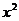 可以取到2a,故当
可以取到2a,故当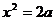 时,
时,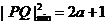
∴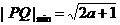
(3)比较a-1与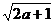 的大小。由
的大小。由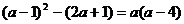
①若a(a-4)<0即0<a<4,又a>1
∴1<a<4时,有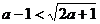
∴最短距离为a-1
②若a(a-4)>0,即a >4时,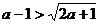 ,最短距离为
,最短距离为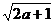
③若a(a-4)=0,即a=4时,最短距离为3
综上所述:a=4时,最短距离为3,
1<a<4时,最短距离为a-1,
a>4时,最短距离为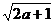
∵PM:MA=3:1
∴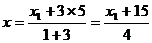 ,
,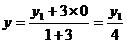
即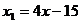 ,
,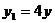 ,又点P在抛物线
,又点P在抛物线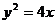 上
上
∴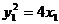
∴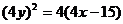
即所求点M的轨迹方程为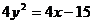
10.提示:由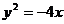 得p=2,焦点(-1,0),直线
得p=2,焦点(-1,0),直线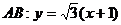
由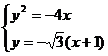 得
得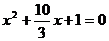 ,易求得
,易求得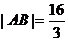
∴△AOB的面积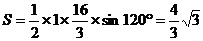
11.试求点P(0,a)(a>1)到曲线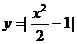 上点的最短距离。
上点的最短距离。
答案与提示
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com