
题目列表(包括答案和解析)
(一)复习提问
前面,大家学习了圆的概念,哪一位同学来回答?
问题1:具有什么性质的点的轨迹称为圆?
平面内与一定点距离等于定长的点的轨迹称为圆(教师在黑板上画一个圆).
问题2:图2-9中哪个点是定点?哪个点是动点?动点具有什么性质?圆心和半径都反映了圆的什么特点?
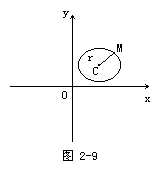
圆心C是定点,圆周上的点M是动点,它们到圆心距离等于定长|MC|=r,圆心和半径分别确定了圆的位置和大小.
问题3:求曲线的方程的一般步骤是什么?其中哪几个步骤必不可少?
求曲线方程的一般步骤为:
(1)建立适当的直角坐标系,用(x,y)表示曲线上任意点M的坐标,简称建系设点;图2-9
(2)写出适合条件P的点M的集合P={M|P(M)|},简称写点集;
(3)用坐标表示条件P(M),列出方程f(x,y)=0,简称列方程;
(4)化方程f(x,y)=0为最简形式,简称化简方程;
(5)证明化简后的方程就是所求曲线的方程,简称证明.
其中步骤(1)(3)(4)必不可少.
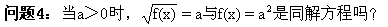
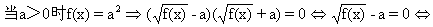
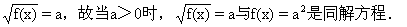
下面我们用求曲线方程的一般步骤来建立圆的标准方程.
2.难点:运用圆的标准方程解决一些简单的实际问题.
(解决办法:使学生掌握分析这类问题的方法是先弄清题意,再建立适当的直角坐标系,使圆的标准方程形式简单,最后解决实际问题.)
1.重点:(1)圆的标准方程的推导步骤;(2)根据具体条件正确写出圆的标准方程.
(解决办法:(1)通过设问,消除难点,并详细讲解;(2)多多练习、讲解.)
(三)学科渗透点
圆基于初中的知识,同时又是初中的知识的加深,使学生懂得知识的连续性;通过圆的标准方程,可解决一些如圆拱桥的实际问题,说明理论既来源于实践,又服务于实践,可以适时进行辩证唯物主义思想教育.
(二)能力训练点
通过圆的标准方程的推导,培养学生利用求曲线的方程的一般步骤解决一些实际问题的能力.
(一)知识教学点
使学生掌握圆的标准方程的特点,能根据所给有关圆心、半径的具体条件准确地写出圆的标准方程,能运用圆的标准方程正确地求出其圆心和半径,解决一些简单的实际问题,并会推导圆的标准方程.
16.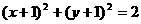 或
或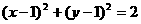 。 提示:充分利用条件中的几何性质,用圆的标准方程求解
。 提示:充分利用条件中的几何性质,用圆的标准方程求解
15.F=3. 提示:设点P、Q两点的坐标,用韦达定理求解
14.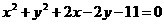
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com