
题目列表(包括答案和解析)
11.方程log3(1-2·3x)=2x+1的解x=_______.
解析:32x+1=1-2·3x,即3(3x)2+2·3x-1=0.
解得3x=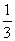 ,故x=-1.
,故x=-1.
答案:-1
10.今有一组试验数据如下:
|
t |
1.99 |
3.0 |
4.0 |
5.1 |
6.12 |
|
v |
1.5 |
4.04 |
7.5 |
12 |
18.01 |
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是
A.v=log2t B.v=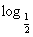 t
t
C.v=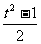 D.v=2t-2
D.v=2t-2
解析:五组数据,取近似值1.99≈2;4.04≈4;5.1≈5,18.01≈18,代入验证可知v=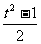 最接近.
最接近.
答案:C
第Ⅱ卷(非选择题 共70分)
9.已知f(x)的图象关于y轴对称,且它在[0,+∞)上是减函数,若f(lgx)>f(1),则x的取值范围是
A.(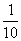 ,1) B.(0,
,1) B.(0,
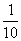 )∪(1,+∞)
)∪(1,+∞)
C.( 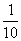 ,10) D.(0,1)∪(10,+∞)
,10) D.(0,1)∪(10,+∞)
解析:若函数f(x)的图象关于y轴对称,则在y轴两侧的对称区间上 ,它们的单调性相反.
由题可知,0≤|lgx|<1,
即-1<lgx<1,lg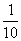 <lgx<lg10,
<lgx<lg10,
所以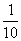 <x<10.
<x<10.
答案:C
8.世界人口已超过56亿,若按千分之一的年增长率计算,则两年增长的人口就可相当于 一个
A.新加坡(270万) B.香港(560万)
C.瑞士(700万) D.上海(1200万)
解析:本题考查指数型函数的应用.
若按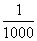 的年增长率计算,则两年后增长的人口数y=560000(1+
的年增长率计算,则两年后增长的人口数y=560000(1+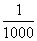 )2-560000≈1120.56(万).
)2-560000≈1120.56(万).
答案:D
7.若函数y=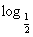 (2-log2x)的值域是(-∞,0),则其定义域是
(2-log2x)的值域是(-∞,0),则其定义域是
A.x<2 B.0<x<2
C.0<x<4 D.2<x<4
解析:令2-log2x=u,由题意知u>1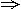 log2x<1,故0<x<2.
log2x<1,故0<x<2.
答案:B
6.已知f(x)=ax,g(x)=logax(a>0且a≠1),若f(3)g(3)<0,则f(x)与g(x)在同一坐标系内的图象可能是

解析:∵f(3)=a3>0,∴g(3)=loga3<0.
∴0<a<1.
答案:C
5.当函数f(x)=2-|x-1|-m的图象与x轴有交点时,实数m的取值范围是
A.-1≤m<0 B.0≤m≤1
C.0<m≤1 D.m≥1
解析:函数f(x)=2-|x-1|-m的图象与x轴有交点,即方程2-|x-1|-m=0有解,∴m=2-|x-1|.
∴0<m≤1.
答案:C
4.已知函数f(x)=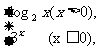 则f[f(
则f[f(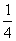 )]的值是
)]的值是
A.9 B.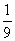
C.-9 D.-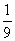
解析:f(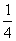 )=log2
)=log2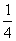 =-2,
=-2,
f(-2)=3-2=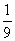 .
.
答案:B
3.设1<x<a,那么logax2、(logax)2、loga(logax)之间的大小顺序是
A.logax2<(logax)2<loga(logax)
B.logax2<loga(logax)<(logax)2
C.loga(logax)<(logax)2<logax2
D.(logax)2<logax2<loga(logax)
解法一:令x=2,a=4,则logax2=log44=1,
(logax)2=(log42)2=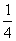
loga(logax)=log4(log42)=-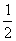 ,
,
∴loga(logax)<(logax)2<logax2.
解法二:∵1<x<a,∴0<logax<1.
logax2=2logax>logax>0,
0<(logax)2<logax,loga(logax)<loga1=0,
∴loga(logax)<(logax)2<logax2.
答案:C
2.若a、b是任意实数,且a>b,则
A.a2>b2 B.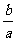 <1
<1
C.lg(a-b)>0 D.(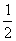 )a<(
)a<(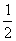 )b
)b
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com