1．下列说法正确的是(　　 )

　A、若a＞b，c＞d，则ac＞bd　　　　　　 B、若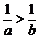，则a＜b

C、若b＞c，则|a|·b≥|a|·c　　　　　　　 D、若a＞b，c＞d，则a-c＞b-d

20．(12分)已知抛物线y²=4ax(0＜a＜1)的焦点为F，以A(a+4,0)为圆心，｜AF｜为半径在x轴上方作半圆交抛物线于不同的两点M和N，设P为线段MN的中点．　　　　　　　　　　　　　　　　　

(1)求｜MF｜+｜NF｜的值；

(2)是否存在这样的a值，使｜MF｜、｜PF｜、｜NF｜成等差数列?如存在，求出a的值，若不存在，说明理由.

解：(1)F(a,0),设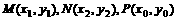，由{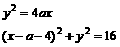

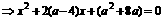，　…………………………3分

，

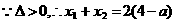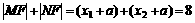
　　　　　　　　 …………………………6分

(2)假设存在a值，使的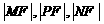成等差数列，

即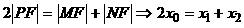　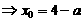 　①，

　　　　　　　　　　　　　　 ………………………8分

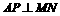
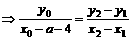∵P是圆A上两点M、N 所在弦的中点，∴，　 …………………………10分

由①得：

，

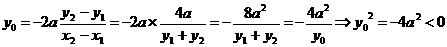这是不可能的．　　　　　　　 …………………………11分

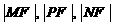∴假设不成立．即不存在a值，使的成等差数列．

　　　　　　　　　　　　　　 …………………………12分

19.(13分)已知数列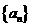满足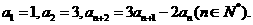

　　　 (I)证明：数列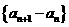是等比数列；

　　　 (II)求数列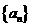的通项公式；

(I)证明：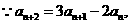

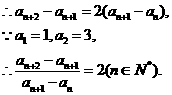
………………………7分

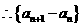是以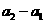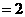为首项，2为公比的等比数列。

……………………8分

(II)解：由(I)得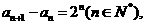……………………10分　　

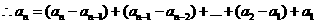
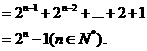
……………………………………13分

18.(13分)记函数f(x)=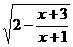的定义域为A,　 g(x)=lg[(x－a－1)(2a－x)]　 (a<1) 的定义域为B.

(Ⅰ) 求A；

(Ⅱ) 若BA, 求实数a的取值范围.

解：(Ⅰ)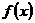 的定义域满足不等式2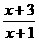－≥0, …………………2分

得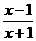≥0, 　　x <－1或x ≥1　　　　　 　…………………………6分

即A=(－∞,－1)∪[1,+ ∞)　 …………………………7分

(Ⅱ) 条件BA表明,集合B是集合A成立的充分条件,首先要求出集合B.

由(x－a－1)(2a－x)>0,　　　　　　 …………………………9分

得(x－a－1)(x－2a)<0.

∵a<1,　 ∴a+1>2a,

∴B=(2a,a+1).　　　　　　　　　 …………………………11分

∵BA, ∴2a≥1或a+1≤－1,

　即a≥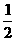或a≤－2, 而a<1,

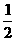∴≤a<1或a≤－2, 　　　　　…………………………12分

故当BA时, 实数a的取值范围是.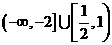

…………………………13分

17. (14分)如图在⊿MNG中，己知NO=GO=2，当动点M满足条件sinG-sinN=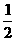sinM时，求动点M的轨迹方程．y

　　　　　　　　　　　　　　　　 　　　　　　　　M

　　　　　　　　　 　　　　　　　　　　　　　　　　x　　　　　　　　　

　　　　　　　 　　　　　　　　　　　　　N　　 O　　 　G　

　解：∵sinG-sinN=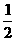sinM，

∴由正弦定理，得｜MN|-|MG|=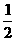×4．…………………………5分

∴由双曲线的定义知,点M的轨迹是以N、G为焦点的双曲线的右支(除去与x轴的交点)．　　 …………………………10分

∴2c=4,2a=2，即c=2,a=1.

∴b²=c²-a²=3．　　　　　　　 …………………………12分

∴动点M的轨迹方程为：x²-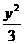=1(x>0,且y≠0)………………14分

16．(14分)抛物线的焦点F在x轴的正半轴上，A(m，-3)在抛物线上，且|AF|=5,求抛物线的标准方程．

　解：设抛物线的方程为y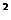＝2px(p>0) , …………………………2分

∵A点在抛物线上，∴(-3)² =2pm ∴m=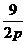①, ………………4分又|AF|=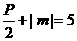②,　　　　　 …………………………9分

把①代入②可得: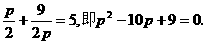 ………………12分∴p=1或p=9　　 ………………13分

∴所求的抛物线方程为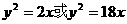………………………14分

15.(14分)已知等比数列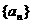的前n项和记为 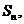　a₃=3 , a₁₀=384.

求该数列的公比q和通项a_n

　解:　 由a₁₀₌ a₃q⁷　 得q⁷=128, ∴q=2 ………………………7分

又a₃=3得a₁q²=3 ∴ a₁=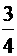　　 ………………………10分∴ a_n=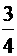×2^n-1=3·2^n-3…………………………………14分

13、　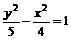 　　　　14、　　 1　　　

11、　　　 16　　　　　 12、

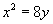
14．若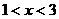，则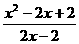的最小值是___________. 1　　　　

高二数学(文科)上册期末考试题