
题目列表(包括答案和解析)
4.已知A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC是
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形
3.给出以下四个命题
①过空间一点有且只有一个平面与两条异面直线都平行
②过两条异面直线中的一条有且只有一个平面与另一条直线平行
③过两条异面直线中的一条有且只有一个平面与另一条直线垂直
④与两条异面直线都相交的两条直线是异面直线
其中真命题的个数为
A.4 B.3 C.2 D.1
2.空间四边形ABCD中,AB=CD,AB与CD成30°角,E、F分别为BC、AD的中点,则EF和AB所成角为
A.15° B.75° C.15°或75° D.30°
1.已知α,β,γ是两两相交的三个平面,则α∩β∩γ等于
A.一个点 B.一条直线
C. D.以上三种情况均有可能
D.以上三种情况均有可能
22.(本小题满分14分)
已知圆C: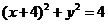 ,圆D的圆心D在y轴上,且与圆C外切,圆D与y轴交于A 、B两点,点P(-3,0)
,圆D的圆心D在y轴上,且与圆C外切,圆D与y轴交于A 、B两点,点P(-3,0)
(1)若点D的坐标为(0,3),求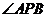 的正切值;
的正切值;
(2)当点D在y 轴上运动时,求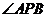 的最大值;
的最大值;
(3)在x轴上是否存在定点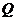 ,当圆D在y轴上运动时,
,当圆D在y轴上运动时,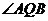 是定值?如果存在,求点
是定值?如果存在,求点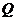 的坐标,如果不存在,说明理由.
的坐标,如果不存在,说明理由.
21.(本小题满分12分)
已知圆的方程是: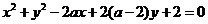 ,其中
,其中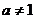 ,且
,且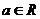 .
.
(1)求证: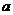 取不为1的实数时,上述圆恒过定点;
取不为1的实数时,上述圆恒过定点;
(2)求恒与圆相切的直线的方程;
(3)求圆心的轨迹方程。
20.(本小题满分12分)
已知定点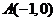 、
、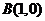 ,动点
,动点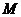 满足:
满足: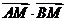 等于点
等于点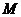 到点
到点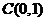 距离平方的k倍.
距离平方的k倍.
(1)试求动点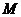 的轨迹方程;
的轨迹方程;
(2)当k=2时,求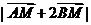 最大值和最小值.
最大值和最小值.
19.(本小题满分12分)
某人上午7:00时,乘摩托车以匀速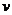 千米/时
千米/时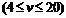 从A港出发到相距50千米的B港去,然后乘汽车以匀速
从A港出发到相距50千米的B港去,然后乘汽车以匀速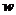 千米/时
千米/时 自B港向距300千米的C市驶去,要求在当天16:00时至21:00时这段时间到达C市.设汽车所需要的时间为x小时, 摩托车所需要的时间为y小时.
自B港向距300千米的C市驶去,要求在当天16:00时至21:00时这段时间到达C市.设汽车所需要的时间为x小时, 摩托车所需要的时间为y小时.
(1)作图表示满足上述条件的x, y的范围;
(2)如果已知所要的经费: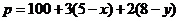 (元),那么
(元),那么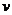 ,
, 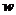 分别是多少时所要的经费最少?此时需花费多少元?
分别是多少时所要的经费最少?此时需花费多少元?
18.(本小题满分12分)
设直线l与圆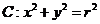 交于A、B两点,O为坐标原点,已知
交于A、B两点,O为坐标原点,已知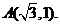
(1)当原点O到直线l的距离为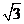 时,求直线l的方程;
时,求直线l的方程;
(2)当OA⊥OB时,求直线l的方程.
17.(本小题满分12分)
已知A(1,2),B(5,4)和直线x-2y-2=0上一动点P,且点P使|PA|+|PB|最小,求点P的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com