
题目列表(包括答案和解析)
考试要求:1、理解向量的概念,掌握向量的几何表示,了解共线向量的概念。2、掌握向量的加法和减法。3、掌握实数与向量的积,理解两个向量共线的充要条件。4、了解平面向量的基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算。5、掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直问题,掌握向量垂直的条件。6、掌握平面两点间的距离公式,以及线段的定比分点和中点坐标公式,并且能熟练运用,掌握平移公式。
1、已知向量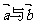 不共线,且
不共线,且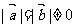 ,则下列结论中正确的是
,则下列结论中正确的是
A.向量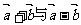 垂直 B.向量
垂直 B.向量 与
与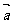 垂直
垂直
C.向量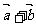 与
与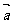 垂直 D.向量
垂直 D.向量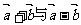 共线
共线
7.线段的定比分点:
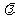 的符号与分点P的位置之间的关系:当P点在线段 P
的符号与分点P的位置之间的关系:当P点在线段 P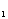 P
P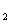 上时
上时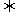
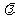 >0;当P点在线段
P
>0;当P点在线段
P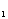 P
P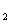 的延长线上时
的延长线上时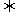
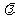 <-1;当P点在线段P
<-1;当P点在线段P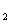 P
P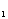 的延长线上时
的延长线上时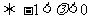 ;若点P分有向线段
;若点P分有向线段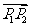 所成的比为
所成的比为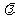 ,则点P分有向线段
,则点P分有向线段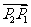 所成的比为
所成的比为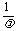 。
。
6、向量的运算:
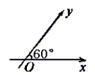
如图,在平面斜坐标系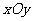 中,
中,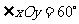 ,平面上任一点P关于斜坐标系的斜坐标是这样定义的:若
,平面上任一点P关于斜坐标系的斜坐标是这样定义的:若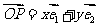 ,其中
,其中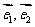 分别为与x轴、y轴同方向的单位向量,则P点斜坐标为
分别为与x轴、y轴同方向的单位向量,则P点斜坐标为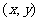 。
。
4、平面向量的数量积:
(1)两个向量的夹角:对于非零向量 ,
,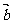 ,作
,作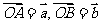 ,
,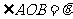
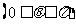 称为向量
称为向量 ,
,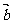 的夹角,当
的夹角,当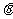 =0时,
=0时, ,
,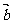 同向,当
同向,当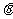 =
=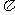 时,
时, ,
,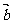 反向,当
反向,当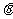 =
=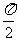 时,
时, ,
,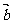 垂直。
垂直。
当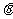 为锐角时,
为锐角时,

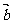 >0,且
>0,且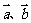 不同向,
不同向,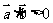 是
是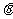 为锐角的必要非充分条件;当
为锐角的必要非充分条件;当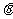 为钝角时,
为钝角时,

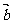 <0,且
<0,且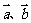 不反向,
不反向,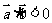 是
是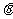 为钝角的必要非充分条件;
为钝角的必要非充分条件;
 (2)
(2)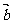 在
在 上的投影为
上的投影为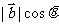 ,它是一个实数,但不一定大于0。
,它是一个实数,但不一定大于0。
3. 实数与向量的积:实数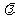 与向量
与向量 的积是一个向量,记作
的积是一个向量,记作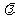
 ,它的长度和方向规定如下:
,它的长度和方向规定如下: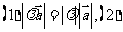 当
当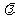 >0时,
>0时,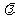
 的方向与
的方向与 的方向相同,当
的方向相同,当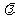 <0时,
<0时,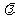
 的方向与
的方向与 的方向相反,当
的方向相反,当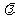 =0时,
=0时,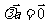 ,注意:
,注意: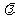
 ≠0。
≠0。
2、向量的表示方法:
(1)几何表示法:用带箭头的有向线段表示,如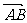 ,注意起点在前,终点在后;
,注意起点在前,终点在后;
(2)符号表示法:用一个小写的英文字母来表示,如 ,
,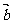 ,
,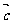 等;
等;
(3)坐标表示法:在平面内建立直角坐标系,以与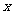 轴、
轴、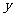 轴方向相同的两个单位向量
轴方向相同的两个单位向量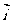 ,
,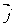 为基底,则平面内的任一向量
为基底,则平面内的任一向量 可表示为
可表示为
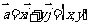 ,称
,称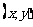 为向量
为向量 的坐标,
的坐标, =
=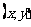 叫做向量
叫做向量 的坐标表示。如果向量的起点在原点,那么向量的坐标与向量的终点坐标相同。
的坐标表示。如果向量的起点在原点,那么向量的坐标与向量的终点坐标相同。
1、向量有关概念:
(1)向量的概念
向量常用有向线段来表示,注意不能说向量就是有向线段,为什么?(向量可以平移)。
(2)零向量:长度为0的向量叫零向量,记作: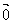 ,注意零向量的方向是任意的;
,注意零向量的方向是任意的;
(3)单位向量:长度为一个单位长度的向量叫做单位向量(与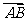 共线的单位向量是
共线的单位向量是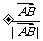 );
);
(4)相等向量:长度相等且方向相同的两个向量叫相等向量,相等向量有传递性;
(5)平行向量(也叫共线向量):方向相同或相反的非零向量 、
、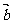 叫做平行向量,记作:
叫做平行向量,记作: ∥
∥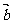 ,规定零向量和任何向量平行。
,规定零向量和任何向量平行。
提醒:①相等向量一定是共线向量,但共线向量不一定相等;②两个向量平行与与两条直线平行是不同的两个概念:两个向量平行包含两个向量共线, 但两条直线平行不包含两条直线重合;
③平行向量无传递性!(因为有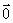 );
);
④三点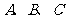 共线
共线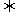
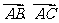 共线;
共线;
(6)相反向量:长度相等方向相反的向量叫做相反向量。 的相反向量是-
的相反向量是- 。
。
15. 三角形五“心”向量形式的充要条件
设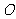 为
为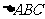 所在平面上一点,角
所在平面上一点,角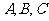 所对边长分别为
所对边长分别为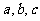 ,则
,则
(1)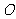 为
为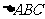 的外心
的外心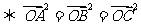 .
.
(2)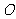 为
为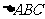 的重心
的重心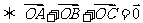 .
.
(3)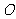 为
为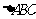 的垂心
的垂心
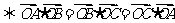 .
.
(4)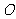 为
为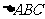 的内心
的内心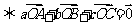 .
.
(5)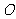 为
为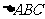 的
的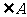 的旁心
的旁心
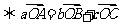 .
.
14.“按向量平移”的几个结论
(1)点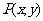 按向量a=
按向量a=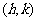 平移后得
平移后得
到点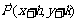 .
.
(2) 函数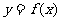 的图象
的图象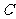 按向量a=
按向量a=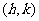 平移后得到图象
平移后得到图象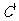 ,则
,则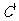 的函数解析式为
的函数解析式为
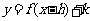 .
.
(3) 图象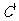 按向量a=
按向量a=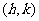 平移后得到图象
平移后得到图象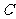 ,若
,若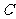 的解析式
的解析式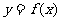 ,则
,则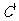 的函数解析式为
的函数解析式为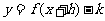 .
.
(4)曲线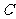 :
: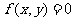 按向量a=
按向量a=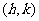 平移后得到图象
平移后得到图象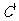 ,则
,则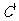 的方程为
的方程为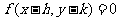 .
.
(5) 向量m=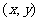 按向量a=
按向量a=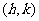 平移后得到的向量仍然为m=
平移后得到的向量仍然为m=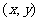 .
.
注意:(1)函数按向量平移与平常“左加右减”有何联系?(2)向量平移具有坐标不变性,可别忘了啊!
13.点的平移公式

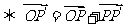
注:图形F上的任意一点P(x,y)在平移后图形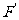 上的对应点为
上的对应点为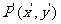 ,且
,且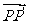 的坐标为
的坐标为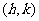 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com