
题目列表(包括答案和解析)
21. ( 本小题满分14分)
已知 函数f(x)=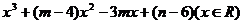 的图像关于原点对称,其中m,n为实常数。
的图像关于原点对称,其中m,n为实常数。
(1) 求m , n的值;
(2) 试用单调性的定义证明:f (x) 在区间[-2, 2] 上是单调函数;
(3) [理科做] 当-2≤x≤2 时,不等式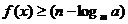 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
20. 随着我国加入WTO,某企业决定从甲、乙两种产品中选择一种进行投资生产,打入国际市场。已知投资生产这两种产品的有关数据如下表(单位:万美元)
 项 目 项 目类 别 |
年固定成本 |
每件产品成本 |
每件产品销售价 |
每年最多生产的件数 |
|
甲产品 |
30 |
a |
10 |
200 |
|
乙产品 |
50 |
8 |
18 |
120 |
其中年固定成本与生产的件数无关,a为常数,且4≤a≤8。令外,年销售x件乙产品时需上交0.05x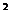 万美元的特别关税。
万美元的特别关税。
(1)
写出该厂分别投资生产甲、乙两种产品的年利润y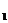 ,y
,y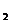 与生产相应产品的件数x (x
与生产相应产品的件数x (x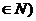 之间的函数关系式;
之间的函数关系式;
(2) 分别求出投资生产这两种产品的最大年利润;
(3) 如何决定投资可获最大年利润。
.
19. .( 本小题满分14分)
设数列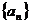 前项和为
前项和为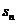 ,且(3
,且(3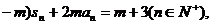 ,其中m为常数,m
,其中m为常数,m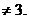
(1) 求证:是等比数列;
(2) 若数列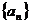 的公比q=f(m),数列
的公比q=f(m),数列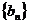 满足
满足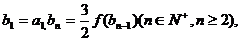 求证:
求证: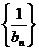 为等差数列,求
为等差数列,求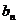 .
.
18.( 本小题满分14分)
经过抛物线y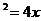 的焦点F的直线L与该抛物线交于A,B两点.
的焦点F的直线L与该抛物线交于A,B两点.
(1) 若线段AB的斜率为k,试求中点M的轨迹方程;
(2)
若直线的斜率k>2,且点M到直线3 x+4y+m=0的距离为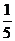 ,试确定m的取值范围。
,试确定m的取值范围。
17.
 .( 本小题满分12分)
.( 本小题满分12分)
如图,正三角形ABC与直角三角形BCD成直二面角,
且∠BCD=90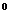 ,∠CBD=30
,∠CBD=30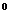 .
.

 (1) 求证:AB⊥CD;
B
C
(1) 求证:AB⊥CD;
B
C
(2)求二面角D-AB-C的正切值。 D
(3) 求异面直线AC和BD所成的角。
16.( 本小题满分12分)
已知复数z=sinB+(1-cosB)i ,argz=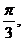 A, B, C是⊿ABC的内角。
A, B, C是⊿ABC的内角。
(1)求B; (2)求sinA+sinC的取值范围。
.
A
15.已知双曲线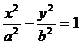 的左支上存在一点P到左焦点的距离是点P到右焦点距离和到左准线距离的比例中项,则双曲线的离心率e的取值范围是
.
的左支上存在一点P到左焦点的距离是点P到右焦点距离和到左准线距离的比例中项,则双曲线的离心率e的取值范围是
.
14.某校有学生宿舍若干间,现安排高三女生居住,若每间住5人,余60人. 若每间住10人,则有一间宿舍不空也不满,则高三女生有 人,宿舍有 间.
13.一个圆柱形容器的内半径为5cm,两个直径为5的玻璃小球被浸没于容器的水中,当取出这两个小球后, 容器的水面下降了x cm, 则x= .
12.
 在下面等号右侧两个分数的分母方块处,各填上一个自然数,并且使这两个自然数的和最小:1=
在下面等号右侧两个分数的分母方块处,各填上一个自然数,并且使这两个自然数的和最小:1=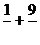 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com