
题目列表(包括答案和解析)
19.(本小题满分12分)
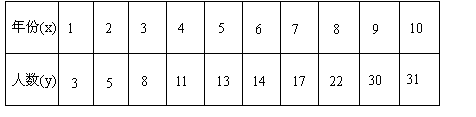
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村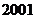 到
到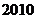 年十年间每年考入大学的人数.为方便计算,
年十年间每年考入大学的人数.为方便计算,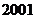 年编号为
年编号为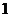 ,
,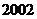 年编号为
年编号为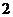 ,…,
,…,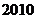 年编号为
年编号为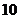 .数据如下:
.数据如下:
(Ⅰ)从这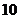 年中随机抽取两年,求考入大学人数至少有
年中随机抽取两年,求考入大学人数至少有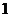 年多于
年多于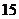 人的概率;
人的概率;
(Ⅱ)根据前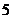 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出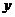 关于
关于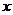 的回归方程
的回归方程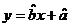 ,并计算第
,并计算第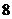 年的估计值和实际值之间的差的绝对值.
年的估计值和实际值之间的差的绝对值.
18.(本小题满分12分)
 已知三棱柱
已知三棱柱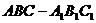 ,底面三角形
,底面三角形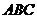 为正三角形,侧棱
为正三角形,侧棱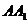
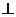 底面
底面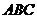 ,
, 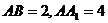 ,
,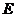 为
为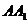 的中点,
的中点,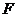 为
为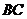 中点.
中点.
(Ⅰ) 求证:直线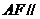 平面
平面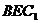 ;
;
(Ⅱ)求平面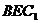 和平面
和平面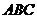 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
17.(本小题满分12分)
已知函数 .
.
(Ⅰ) 求函数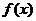 的单调递增区间;
的单调递增区间;
(Ⅱ) 已知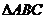 中,角
中,角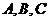 所对的边长分别为
所对的边长分别为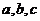 ,若
,若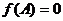 ,
,
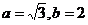 ,求
,求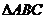 的面积
的面积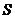 .
.
16. 若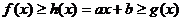 ,则定义
,则定义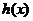 为曲线
为曲线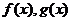 的
的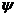 线.已知
线.已知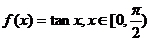 ,
,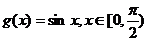 ,则
,则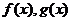 的
的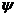 线为
线为 .
.
15. 已知集合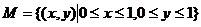 表示的区域为
表示的区域为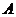 ,
,
集合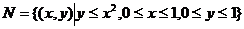 表示的区域为
表示的区域为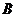 ,
,
向区域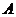 内随机抛掷一粒豆子,则豆子落在区域
内随机抛掷一粒豆子,则豆子落在区域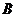 内的概率为
内的概率为 .
.
14. 已知三棱锥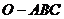 ,
,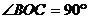 ,
,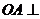 平面
平面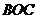 ,其中
,其中
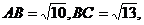
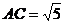 ,
,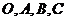 四点均在球
四点均在球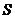 的表面上,则球
的表面上,则球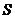 的
的
表面积为 .
.
13. 某市有三类医院,甲类医院有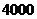 病人,乙类医院有
病人,乙类医院有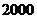 病人,丙类医院有
病人,丙类医院有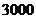 病人,为调查三类医院的服务态度,利用分层抽样的方法抽取
病人,为调查三类医院的服务态度,利用分层抽样的方法抽取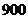 人进行调查,则从乙类医院抽取的人数为
人进行调查,则从乙类医院抽取的人数为 人.
人.
12. 已知抛物线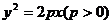 ,
,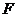 为其焦点,
为其焦点,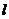 为其准线,过
为其准线,过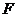 任作一条直线交抛物线于
任作一条直线交抛物线于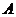 、
、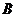 两点,
两点,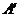 、
、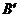 分别为
分别为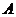 、
、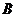 在
在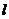 上的射影,
上的射影,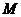 为
为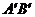 的中点,给出下列命题:
的中点,给出下列命题:
①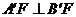 ;
;
②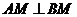 ;
;
③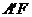 ∥
∥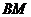 ;
;
④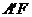 与
与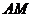 的交点在
的交点在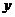 轴上;
轴上;
⑤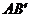 与
与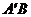 交于原点.
交于原点.
其中真命题的个数为
A.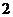 个 B.
个 B.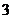 个 C.
个 C.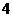 个 D.
个 D.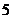 个
个
第Ⅱ卷 (非选择题, 共90分)
11.已知二面角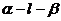 的平面角为
的平面角为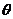 ,点
,点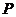 在二面角内,
在二面角内,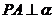 ,
,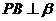 ,
,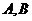 为垂足,且
为垂足,且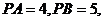 设
设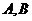 到棱
到棱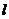 的距离分别为
的距离分别为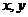 ,当
,当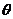 变化时,点
变化时,点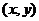 的轨迹方程是
的轨迹方程是
A.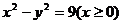 B.
B.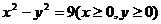
C.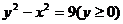 D.
D.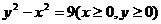
10.设不等式组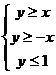 表示的平面区域为
表示的平面区域为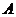 ,不等式
,不等式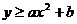 (
(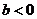 ,
,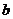 为常数)表示的平面区域为
为常数)表示的平面区域为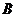 ,
,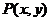 为平面上任意一点,
为平面上任意一点,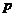 :点
:点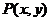 在区域
在区域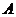 内,
内,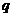 :点
:点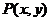 在区域
在区域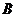 内,若
内,若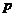 是
是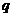 的充分不必要条件,则
的充分不必要条件,则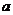 的取值范围是
的取值范围是
A.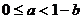 B.
B.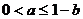 C.
C.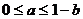 D.
D.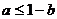
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com