
题目列表(包括答案和解析)
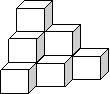
5.如图所示,棱长为1cm的小正方体组成如图所示的几何体,那么这个几何体的
表面积是
|
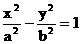 (a>0,b>0)的左、右焦点,P为双曲线上的一点,若
(a>0,b>0)的左、右焦点,P为双曲线上的一点,若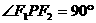 ,且
,且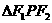 的三边长成等差数列,
的三边长成等差数列,
则双曲线的离心率是 。
4. 已知实数
已知实数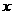 、
、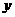 满足约束条件
满足约束条件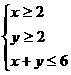 ,则
,则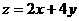 的最大值为 。
的最大值为 。
3.函数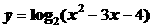 的单调增区间是
。
的单调增区间是
。
2. 命题“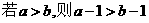 ”的否命题是
。
”的否命题是
。
1.已知集合 =
=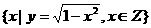 ,
,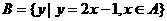 ,则
,则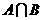 = 。
= 。
24.(本小题10分)选修4-5:不等式选讲
设函数f(x)=x2-x+1,实数a满足|x-a|<1,求证:|f(x)-f(a)|<2(|a|+1).
解析:∵f(x)=x2-x+1,|x-a|<1,
∴|f(x)-f(a)|=|x2-x-a2+a|=|x-a|·|x+a-1|<|x+a-1|=|(x-a)+2a-1|≤|x-a|+|2a+1|<1+|2a|+1=2(|a|+1).
23.(本小题10分)选修4-4:坐标系与参数方程
极坐标方程为ρcosθ-ρsinθ-1=0的直线与x轴的交点为P,与椭圆(θ为参数)交于A,B两点,求PA·PB.
解析:直线ρcosθ-ρsinθ-1=0的斜率为1,
令θ=0,得ρ=1,
∴直线与x轴交于点(1,0)点,
∴直线的参数方程为(t为参数)①
椭圆的普通方程为:x2+4y2=4,②
①代入②得:5t2+2t-6=0,
∵Δ>0,∴PA·PB=|t1·t2|=.
22.(本小题10分)选修4-1:几何证明选讲
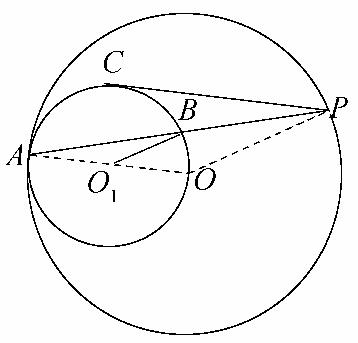
如图,
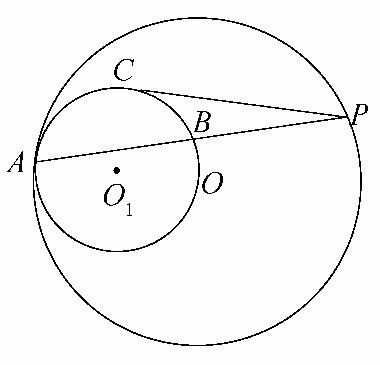
已知⊙O和⊙O1内切于点A,⊙O的弦AP交⊙O1于点B,PC切⊙O1于点C,且=,则⊙O1和⊙O的半径的比值为多少?
解析:如图,连接OP、OA、O1B,ΔOPA和ΔO1BA是顶角相等的等腰三角形,故∠APO=∠ABO1,从而O1B∥OP,故=.
又由切割线定理,知PC2=PB·PA=(PA-AB)·PA=PA2-PA·AB,两端同除以PA2,得=1-,即()2=1-,故=,从而⊙O1和⊙O的半径的比值为==.
21.(本小题14分)已知点F1(-1,0),F2(1,0),动点A到点F1的距离是2,线段AF2的中垂线l交AF1于点P.
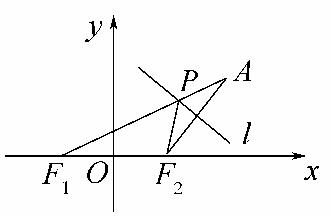
(1)当点A变化时,求动点P的轨迹G的方程;
(2)过点F1、F2分别作互相垂直的两条直线分别与轨迹G交于点D、E和点M、N,试求四边形DMEN的面积的最大值和最小值.
解析:(1)如图,
|AF1|=2,
∴|PA|+|PF1|=2,
又∵|PA|=|PF2|,
∴|PF1|+|PF2|=2,
由椭圆的定义可知动点P的轨迹G的方程为+=1.
(2)当直线DE与x轴垂直时,|DE|=,
此时|MN|=2,四边形DMEN的面积为=4,
同理,当MN与x轴垂直时,也有四边形DMEN的面积为=4.
当直线DE,MN与x轴均不垂直时,设直线DE的方程为
y=k(x+1)(k≠0),代入椭圆方程,消去y,得(2+3k2)x2+6k2x+3k2-6=0.
设D点的坐标为(x1,y1),E点的坐标为(x2,y2),
则)
∴|x1-x2|==,
∴|DE|=|x1-x2|=.
同理,|MN|==.
∴四边形DMEN的面积
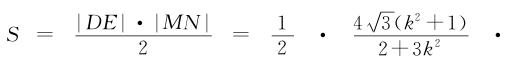
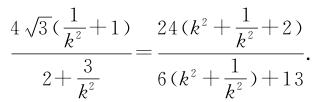
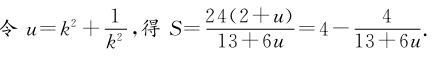
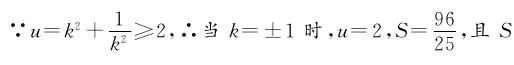

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com