
题目列表(包括答案和解析)
3. 若a∈R,则“a=1”是“|a|=1”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分又不必要条件
2. i是虚数单位1+i3等于
A.i B.-i C.1+i D.1-i
1. 若集合M={-1,0,1},N={0,1,2},则M∩N等于
A.{0,1} B.{-1,0,1}
C.{0,1,2} D.{-1,0,1,2}
(17)(本小题满分12分)
等比数列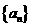 的各项均为正数,且
的各项均为正数,且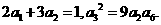
(Ⅰ)求数列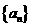 的通项公式;
的通项公式;
(Ⅱ)设 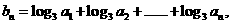 求数列
求数列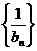 的前n项和.
的前n项和.
(18)(本小题满分12分)
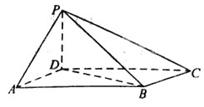 如图,四棱锥P-ABCD中,底面ABCD为平行四
如图,四棱锥P-ABCD中,底面ABCD为平行四
边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅰ)证明:PA⊥BD;
(Ⅱ)若PD=AD,求二面角A-PB-C的余弦值。
(19)(本小题满分12分)
某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品,现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
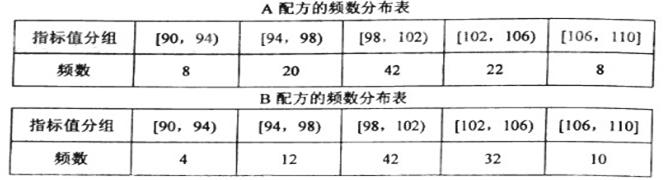
(Ⅰ)分别估计用A配方,B配方生产的产品的优质品率;
(Ⅱ)已知用B配方生成的一件产品的利润y(单位:元)与其质量指标值t的关系式为
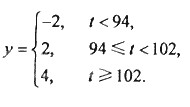
从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
(20)(本小题满分12分)
在平面直角坐标系xOy中,已知点A(0,-1),B点在直线y = -3上,M点满足 ,
, 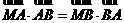 ,M点的轨迹为曲线C。
,M点的轨迹为曲线C。
(Ⅰ)求C的方程;
(Ⅱ)P为C上的动点,l为C在P点处得切线,求O点到l距离的最小值。
(21)(本小题满分12分)
已知函数 ,曲线
,曲线 在点
在点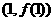 处的切线方程为
处的切线方程为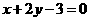 。
。
(Ⅰ)求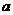 、
、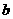 的值;
的值;
(Ⅱ)如果当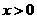 ,且
,且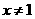 时,
时,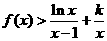 ,求
,求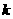 的取值范围。
的取值范围。
请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分。做答时请写清题号。
 (22)(本小题满分10分)选修4-1:几何证明选讲
(22)(本小题满分10分)选修4-1:几何证明选讲
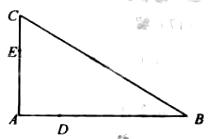
如图,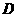 ,
,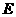 分别为
分别为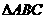 的边
的边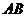 ,
, 上的点,且不与
上的点,且不与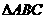 的顶点重合。已知
的顶点重合。已知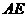 的长为
的长为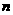 ,
,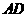 ,
,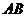 的长是关于
的长是关于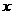 的方程
的方程 的两个根。
的两个根。
(Ⅰ)证明: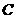 ,
,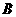 ,
,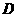 ,
,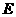 四点共圆;
四点共圆;
(Ⅱ)若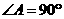 ,且
,且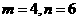 ,求
,求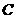 ,
,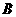 ,
,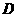 ,
,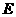 所在圆的半径。
所在圆的半径。
(23)(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系xOy 中,曲线C1的参数方程为
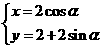 (
(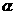 为参数)
为参数)
M是C1上的动点,P点满足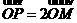 ,P点的轨迹为曲线C2
,P点的轨迹为曲线C2
(Ⅰ)求C2的方程
(Ⅱ)在以O为极点,x 轴的正半轴为极轴的极坐标系中,射线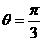 与C1的异于极点的交点为A,与C2的异于极点的交点为B,求
与C1的异于极点的交点为A,与C2的异于极点的交点为B,求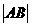 .
.
(24)(本小题满分10分)选修4-5:不等式选讲
设函数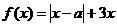 ,其中
,其中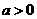 。
。
(Ⅰ)当 时,求不等式
时,求不等式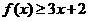 的解集;
的解集;
(Ⅱ)若不等式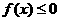 的解集为
的解集为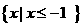 ,求a的值。
,求a的值。
2011年普通高等学校招生全国统一考试
(13)若变量 满足约束条件
满足约束条件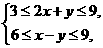 则
则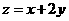 的最小值为 。
的最小值为 。
(14)在平面直角坐标系 中,椭圆
中,椭圆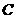 的中心为原点,焦点
的中心为原点,焦点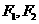 在
在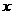 轴上,离心率为
轴上,离心率为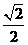 。过
。过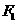 的直线L交C于
的直线L交C于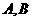 两点,且
两点,且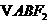 的周长为16,那么
的周长为16,那么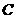 的方程为 。
的方程为 。
(15)已知矩形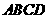 的顶点都在半径为4的球
的顶点都在半径为4的球 的球面上,且
的球面上,且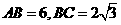 ,则棱锥
,则棱锥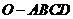 的体积为 。
的体积为 。
(16)在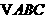 中,
中,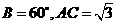 ,则
,则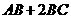 的最大值为 。
的最大值为 。
(1)复数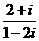 的共轭复数是
的共轭复数是
(A)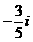 (B)
(B)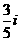 (C)
(C)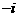 (D)
(D)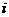
(2)下列函数中,既是偶函数又在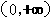 单调递增的函数是
单调递增的函数是
(A)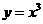 (B)
(B)  (C)
(C)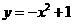 (D)
(D) 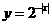
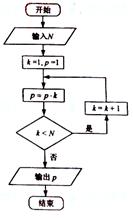 (3)执行右面的程序框图,如果输入的N是6,那么输出的p是
(3)执行右面的程序框图,如果输入的N是6,那么输出的p是
(A)120
(B)720
(C)1440
(D)5040
(4)有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为
(A)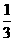 (B)
(B)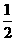 (C)
(C)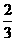 (D)
(D)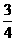
(5)已知角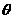 的顶点与原点重合,始边与
的顶点与原点重合,始边与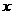 轴的正半轴重合,终边在直线
轴的正半轴重合,终边在直线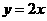 上,则
上,则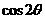 =
=
(A)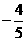 (B)
(B)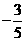 (C)
(C)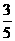 (D)
(D)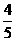
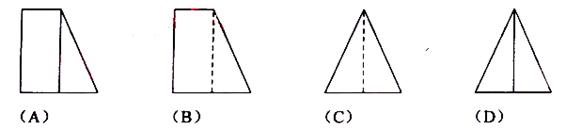
(6)在一个几何体的三视图中,正视图和俯视图如右图所示,
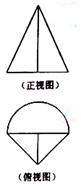 则相应的俯视图可以为
则相应的俯视图可以为
(7)设直线L过双曲线C的一个焦点,且与C的一条对称轴垂直,L与C交于A ,B两点,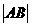 为C的实轴长的2倍,则C的离心率为
为C的实轴长的2倍,则C的离心率为
(A)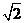 (B)
(B)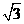 (C)2
(D)3
(C)2
(D)3
(8) 的展开式中各项系数的和为2,则该展开式中常数项为
的展开式中各项系数的和为2,则该展开式中常数项为
(A)-40 (B)-20 (C)20 (D)40
(9)由曲线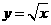 ,直线
,直线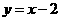 及
及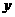 轴所围成的图形的面积为
轴所围成的图形的面积为
(A)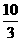 (B)4 (C)
(B)4 (C)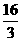 (D)6
(D)6
(10)已知a与b均为单位向量,其夹角为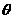 ,有下列四个命题
,有下列四个命题
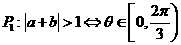
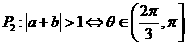
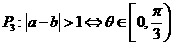
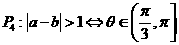
其中的真命题是
(A)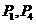 (B)
(B)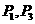 (C)
(C)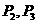 (D)
(D)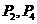
(11)设函数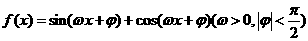 的最小正周期为
的最小正周期为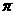 ,且
,且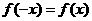 ,则
,则
(A)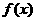 在
在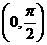 单调递减
(B)
单调递减
(B)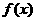 在
在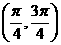 单调递减
单调递减
(C)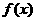 在
在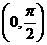 单调递增 (D)
单调递增 (D)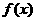 在
在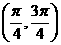 单调递增
单调递增
(12)函数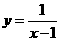 的图像与函数
的图像与函数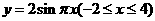 的图像所有交点的横坐标之和等于
的图像所有交点的横坐标之和等于
(A)2 (B) 4 (C) 6 (D)8
第Ⅱ卷
本卷包括必考题和选考题两部分。第13题-第21题为必考题,每个试题考生都必须做答。第22题-第24题为选考题,考生根据要求做答。
12.若集合A={x|x2-2x-8<0},B={x|x-m<0}.
(1)若m=3,全集U=A∪B,试求A∩(∁UB);
(2)若A∩B=∅,求实数m的取值范围;
(3)若A∩B=A,求实数m的取值范围.
解:(1)由x2-2x-8<0,得-2<x<4,
∴A={x|-2<x<4}.
当m=3时,由x-m<0,得x<3,∴B={x|x<3},
∴U=A∪B={x|x<4},∁UB={x|3≤x<4}.
∴A∩(∁UB)={x|3≤x<4}.
(2)∵A={x|-2<x<4},B={x|x<m},
又A∩B=∅,∴m≤-2.
(3)∵A={x|-2<x<4},B={x|x<m},
由A∩B=A,得A⊆B,∴m≥4.
11.已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R}.
(1)若A∩B=[1,3],求实数m的值;
(2)若A⊆∁RB,求实数m的取值范围.
解:A={x|-1≤x≤3},
B={x|m-2≤x≤m+2}.
(1)∵A∩B=[1,3],∴,得m=3.
(2)∁RB={x|x<m-2或x>m+2}.
∵A⊆∁RB,∴m-2>3或m+2<-1.
∴m>5或m<-3.
10.设集合A={x2,2x-1,-4},B={x-5,1-x,9},若A∩B={9},求A∪B.
解:由9∈A,可得x2=9,或2x-1=9,
解得x=±3,或x=5.
当x=3时,A={9,5,-4},B={-2,-2,9},B中元素重复,故舍去;
当x=-3时,A={9,-7,-4},B={-8,4,9},A∩B={9}满足题意,故A∪B=
{-8,-7,-4,4,9};
当x=5时,A={25,9,-4},B={0,-4,9},此时A∩B={-4,9}与A∩B={9}矛盾,故舍去.
综上所述,A∪B={-8,-7,-4,4,9}.
9.某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为________.
解析:借助Venn图分析(如图所示).
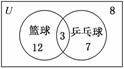
答案:12
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com