
题目列表(包括答案和解析)
23.必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.
已知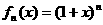 ,
,
(1)若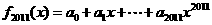 ,求
,求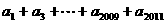 的值;(3分)
的值;(3分)
(2)若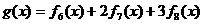 ,求
,求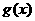 中含
中含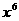 项的系数;(3分)
项的系数;(3分)
(3)证明: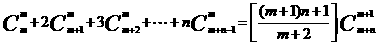 .(4分)
.(4分)
22. 必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.
已知抛物线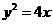 的焦点为
的焦点为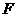 ,直线
,直线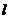 过点
过点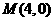 .
.
(1)若点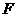 到直线
到直线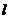 的距离为
的距离为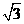 ,求直线
,求直线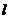 的斜率;(4分)
的斜率;(4分)
(2)设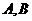 为抛物线上两点,且
为抛物线上两点,且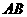 不与
不与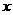 轴垂直,若线段
轴垂直,若线段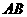 的垂直平分线恰过点
的垂直平分线恰过点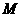 ,求证:线段
,求证:线段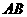 中点的横坐标为定值.(6分)
中点的横坐标为定值.(6分)
21. (选做题)本大题包括A,B,C,D共4小题,请从这4题中选做2小题. 每小题10分,共20分.请在答题卡上准确填涂题目标记. 解答时应写出文字说明、证明过程或演算步骤.
B.选修4-2 矩阵与变换
已知矩阵
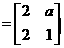 ,其中
,其中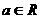 ,若点
,若点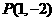 在矩阵
在矩阵 的变换下得到点
的变换下得到点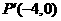 ,
,
(1)求实数a的值;
(2)求矩阵 的特征值及其对应的特征向量.
的特征值及其对应的特征向量.
C.选修4-4 参数方程与极坐标
在平面直角坐标系xOy中,动圆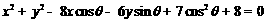 (
(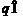 R)的
R)的
圆心为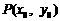 ,求
,求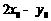 的取值范围.
的取值范围.
20.(本题满分16分)
已知各项均不为零的数列{an}的前n项和为Sn,且满足a1=c,2Sn=anan+1+r.
(1)若r=-6,数列{an}能否成为等差数列?若能,求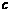 满足的条件;若不能,请说明理由.
满足的条件;若不能,请说明理由.
(2)设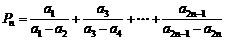 ,
,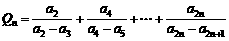 ,
,
若r>c>4,求证:对于一切n∈N*,不等式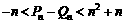 恒成立.
恒成立.
附加题部分
19.(本题满分16分)
已知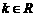 ,函数
,函数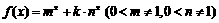 .
.
(1) 如果实数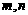 满足
满足 ,函数
,函数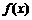 是否具有奇偶性?如果有,求出相应的
是否具有奇偶性?如果有,求出相应的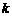
值,如果没有,说明为什么?
(2) 如果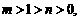 判断函数
判断函数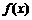 的单调性;
的单调性;
(3) 如果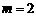 ,
,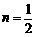 ,且
,且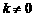 ,求函数
,求函数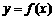 的对称轴或对称中心.
的对称轴或对称中心.
18.(本题满分16分)
如图,直角三角形ABC中,∠B=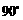 ,AB=1,BC=
,AB=1,BC=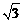 .点M,N分别在边AB和AC
.点M,N分别在边AB和AC
上(M点和B点不重合),将△AMN沿MN翻折,△AMN变为△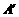 MN,使顶点
MN,使顶点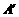 落
落
在边BC上(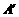 点和B点不重合).设∠AMN=
点和B点不重合).设∠AMN=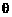 .
.
(1) 用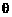 表示线段
表示线段 的长度,并写出
的长度,并写出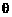 的取值范围;
的取值范围;
 (2) 求线段
(2) 求线段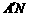 长度的最小值.
长度的最小值.
17.(本题满分14分)
已知椭圆的中心为坐标原点,短轴长为2,一条准线方程为l: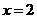 .
.
⑴ 求椭圆的标准方程;
⑵ 设O为坐标原点,F是椭圆的右焦点,点M是直线l上的动点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值.
16.(本题满分14分)
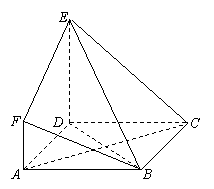
如图, 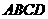 是边长为
是边长为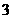 的正方形,
的正方形,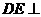 平面
平面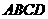 ,
,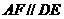 ,
,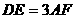 ,
,
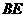 与平面
与平面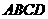 所成角为
所成角为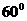 .
.
(1)求证: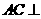 平面
平面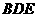 ;
;
(2)设点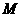 是线段
是线段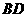 上一个动点,试确定点
上一个动点,试确定点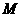 的
的
位置,使得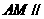 平面
平面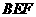 ,并证明你的结论.
,并证明你的结论.
15.(本题满分14分)
在锐角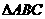 中,角
中,角 ,
,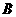 ,
,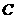 所对的边分别为
所对的边分别为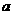 ,
,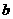 ,
,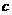 .已知
.已知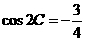 .
.
(1)求 ;(2)当
;(2)当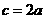 ,且
,且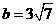 时,求
时,求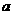 .
.
14.当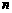 为正整数时,函数
为正整数时,函数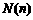 表示
表示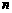 的最大奇因数,如
的最大奇因数,如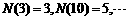 ,
,
设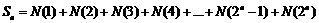 ,则
,则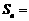 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com