
题目列表(包括答案和解析)
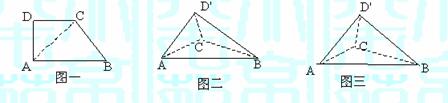
18.(本小题满分12分)在直角梯形ABCD中,ÐD=ÐBAD=90°,AD=DC=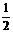 AB=a,(如图一)将△ADC 沿AC折起,使D到
AB=a,(如图一)将△ADC 沿AC折起,使D到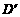 .记面AC
.记面AC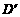 为a,面ABC为b.面BC
为a,面ABC为b.面BC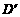 为g.
为g.
(1)若二面角a-AC-b为直二面角(如图二),求二面角b-BC-g的大小;
(2)若二面角a-AC-b为60°(如图三),求三棱锥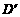 -ABC的体积.
-ABC的体积.
17.(本小题满分12分)如图,四棱锥S-ABCD的底面是边长为1的正方形,
SD垂直于底面ABCD,SB=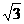 .
.
(1)求证BC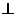 SC;
SC;
(2)求面ASD与面BSC所成二面角的大小;
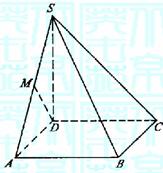 (3)设棱SA的中点为M,求异面直线DM与SB所成角的
(3)设棱SA的中点为M,求异面直线DM与SB所成角的
大小.
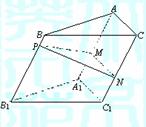
16.(本小题满分12分)如图,点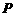 为斜三棱柱
为斜三棱柱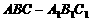 的侧棱
的侧棱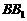 上一点,
上一点,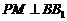 交
交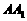 于点
于点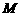 ,
, 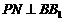 交
交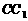 于点
于点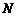 .
.
(1) 求证: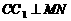 ; (2) 在任意
; (2) 在任意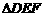 中有余弦定理:
中有余弦定理:
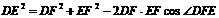 .拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
15.(本小题满分12分)已知SA⊥平面ABC,SA=AB,AB⊥BC,SB=BC,E是SC的中点,
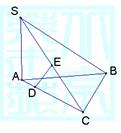 DE⊥SC交AC于D.
DE⊥SC交AC于D.
(1) 求证:SC⊥面BDE;
(2)求二面角E-BD-C的大小.
14.球的半径为8,经过球面上一点作一个平面,使它与经过这点的半径成45°角,则这个平面截球的截面面积为 .
13.在三棱锥P-ABC中,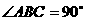 ,
,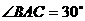 ,BC=5,又PA=PB=PC=AC,则点P到平面ABC的距离是 .
,BC=5,又PA=PB=PC=AC,则点P到平面ABC的距离是 .
12.DABC中ÐACB=90°,PA^平面ABC,PA=2,AC=2,则平面PBC与平面PAC,平面ABC所成的二角的大小分别是______、_________.
11.从平面a外一点P引斜线段PA和PB,它们与a分别成45°和30°角,则ÐAPB的最大值是______最小值是_______
10.已知A(1,1,1),B(-1,0 ,4),C(2 ,-2,3),则〈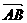 ,
,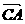 〉的大小为( )
〉的大小为( )
A.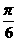 B.
B.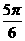 C.
C.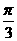 D.
D.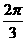
第Ⅱ卷(非选择题,共100分)
9.若正三棱锥的侧面均为直角三角形,侧面与底面所成的角为α,则下列各等式中成立的是 ( )
A.0<α<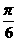 B.
B.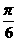 <α<
<α<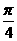 C.
C.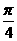 <α<
<α<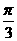 D.
D.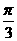 <α<
<α<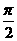
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com