8、根据指令(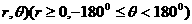机器人在平面上能完成下列动作:先原地旋转角度为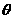(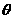为正时,按逆时针方向旋转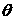,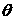为负时,按顺时针方向旋转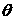－)，再朝其面对的方向沿直线行走距离r。

(1)现机器人在直角坐标系的坐标原点，且x轴正方向，试给机器人下一个指令，使其移动到点(4.4)。

(2)机器人在完成该指令后，发现在点(17,0)处有一小球正向坐标原点作匀速直线滚动，已知小球滚动速度为机器人行走的确倍，若忽略机器人原地旋转所需的时间，问机器人最快在何处截住小球？共给也机器人截住小球所需的指令(结果精确到小数点后两位).

7、如果直线ax + 2y + 2 = 0与直线3x－y－2 = 0平行，那么系数a = (　　 )

　A、－3　　　　 B、－6　　　　 C、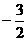　　　　 D、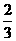

6、将直线l沿x轴正向平移3个单位，沿y轴正向平移5个单位，得直线l＇，再将l＇沿x轴正向平移1个单位，沿y轴负向平移2个单位，恰与l重合。

(1)求直l＇与l之间距离；

(2)当l＇与l关于点(2,3)对称时，求l的方程。

5、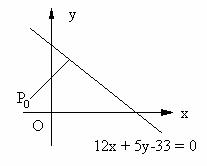如图所示，一个动点P(x,y)以P₀(－2,1)为起点,以v = 2m／s的速度沿着直线12x + 5y－33 = 0垂直的方向向着直线作匀速运动,求P点运动路线的方程,并求出到达给定直线所需时间.

4、以直线l：x + 2y + 1 = 0为对称轴，求与直线l₁：x－y－2 = 0对称的直线l₂的方程。

3、求过两直线l₁：y = 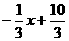和l₂：3x－y = 0的交点，并且与原点距离为1的直线方程。

2、已知直线l₁：x + my + 6 = 0，l₂：(m－2)x + 3y + 2m = 0,m取何值时：

(1) l₁ 与l₂相交；　　 (2) l₁ ⊥l₂；　　 (3) l₁ ∥l₂；　　　 (4) 　l₁ 与l₂重合。

1、求过点A(2，3)，且被两条平行直线3x + 4y－7 = 0和3x + 4y + 8 = 0截得长为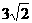的线段的直线方程。

18、直线l过点P(3，4)，并且l在两坐标轴上截距相等，求直线l的方程。

B卷

17、已知二次方程x² + xy－6y²－20x－20y + k = 0表示两条直线，试求k的值与两条直线的方程。