
题目列表(包括答案和解析)
17、解:(1)由已知得: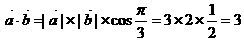 ,……………………3分
,……………………3分
(2)又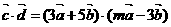
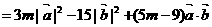 …………………………………………5分
…………………………………………5分
=27m–60+3(5m–9)=0…………………………………………………………7分
解得 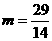 …………………………………………………………………8分
…………………………………………………………………8分
16、设C(x1, y1)、D(x2, y2),由于AC、BD的交点在x轴上,即:AC、BD的中点在x轴上,
所以3+y1=0,4+y2=0,所以y1= –3,y2= –4,……………………………………3分
又AB⊥BC,所以kAB kBC= –1,kAB=–1,
所以kBC = 1,–3–4=x1+2,x1= –9,…………………………………………………5分
同理可得,x2= –8,…………………………………………………………………6分
所以C(–9, –3)、D(–8, –4)。…………………………………………………………8分
11、B 12、A 13、C 14、C 15、A
7、{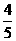 , –
, –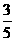 } 8、2x–3y+7=0
9、–1或1 10、15o 或75o
} 8、2x–3y+7=0
9、–1或1 10、15o 或75o
1、0o<q≤90o 2、60o 3、MÌPÌQÌN 4、(–11, 10) 5、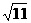 6、–10
6、–10
20、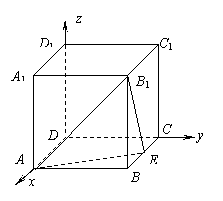 (满分12分) 在正方体ABCD–A1B1C1D1中,E为棱BC的中点。(1) 在棱BB1上是否存在一点M,使D1M⊥平面B1AE?为什么?;(2) 在正方体表面ABB1A1上是否存在一点N,使D1N⊥平面B1AE?为什么?
(满分12分) 在正方体ABCD–A1B1C1D1中,E为棱BC的中点。(1) 在棱BB1上是否存在一点M,使D1M⊥平面B1AE?为什么?;(2) 在正方体表面ABB1A1上是否存在一点N,使D1N⊥平面B1AE?为什么?
金山区2005学年度第一学期期末高二数学试题评分标准
19、(满分9分) 已知向量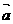 ={1, 2},
={1, 2},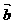 ={x,1},且
={x,1},且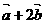 与
与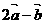 平行,(1) 求向量
平行,(1) 求向量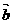 ; (2) 已知点A(3 ,–1),向量
; (2) 已知点A(3 ,–1),向量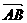 与
与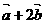 垂直,求直线AB的一般式方程。
垂直,求直线AB的一般式方程。
18、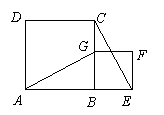 (满分8分) 已知四边形ABCD、BEFG都是正方形,且A、B、E在同一条直线上,用坐标法证明:AG⊥CE。
(满分8分) 已知四边形ABCD、BEFG都是正方形,且A、B、E在同一条直线上,用坐标法证明:AG⊥CE。
17、(满分8分) 若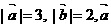 与
与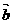 夹角为
夹角为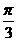 ,
,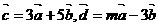 ,(1) 求
,(1) 求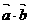 的值;(2)试问
的值;(2)试问 为何值时,
为何值时,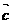 与
与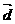 互相垂直。
互相垂直。
16、(满分8分)已知矩形ABCD的两个顶点分别是A(–1, 3)、B(–2,4),若它的对角线的交点在x轴上,求另外两个顶点的坐标。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com