
题目列表(包括答案和解析)
7、
点(a,b)关于直线x+y=0对称的点是 ( )
(A) (-a,-b) (B) (a,-b) (C) (b,a) (D) (-b,-a)
翰林汇
6、
三角形中, 已知三边a,b,c依次所对应的三内角α,β,γ满足lgsinα+lgsinγ=2lgsinβ, 则直线xsin2α+ysinα=α与xsin2β+ysinγ=c的位置关系是 ( )
(A) 平行 (B) 斜交 (C) 垂直 (D) 重合
翰林汇
5、
两平行直线3x+2y-3=0与6x+ky+1=0的距离为 ( )
(A)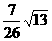 (B)
(B)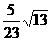 (C)
(C)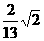 (D)与k值有关
(D)与k值有关
翰林汇
4、
已知点M(0,-1),点N在直线x-y+1=0上,若直线MN垂直于直线x+2y-3=0,则点N坐标是 ( )
(A)(-2,-3) (B)(2,1) (C)(2,3) (D)(-2,-1)
翰林汇
3、
两条直线2x-y+k=0和4x-2y+1=0的位置关系是 ( )
(A)平行 ( B)垂直 (C)相交但不垂直 (D)平行或重合
翰林汇
2、
在线段BA的延长线上,取点P,使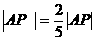 ,则P分AB的比为( )
,则P分AB的比为( )
(A)-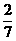 (B)-
(B)-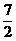 (C)
(C)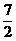 (D)
(D)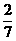
翰林汇
1、
ΔPQR的顶点P(2,-4),Q(-1,2),R(3,4),则ΔPQR的面积是 ( )
(A)12 (B)18 (C)15 (D)24
翰林汇
20、解:不妨设正方体的棱长为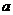 ,则
,则
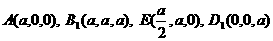 ………………………………………2分
………………………………………2分
又: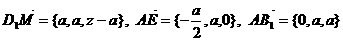 ……………………5分
……………………5分
假设BB1上存在一点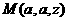 ,使
,使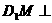 平面B1AE成立,
平面B1AE成立,
则必有: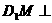 AE;
AE;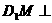 AB1
AB1
所以: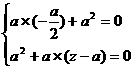 ,此时方程组无解,…………………………………7分
,此时方程组无解,…………………………………7分
故不存在点M,使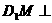 平面B1AE。……………………………………………8分
平面B1AE。……………………………………………8分
(2) 假设正方体表面ABB1A1上存在一点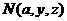 ,使
,使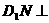 平面B1AE成立。
平面B1AE成立。
则必有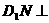 AE;
AE;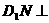 AB1成立。由于
AB1成立。由于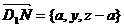 ……………9分
……………9分
所以: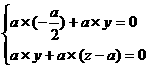 解得
解得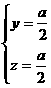 ,……………………………………11分
,……………………………………11分
即存在点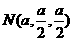 ,也即正方体表面ABB1A1上存在一点N恰是正方形ABB1A1的中心,使
,也即正方体表面ABB1A1上存在一点N恰是正方形ABB1A1的中心,使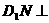 平面B1AE成立。……………………………………………………12分
平面B1AE成立。……………………………………………………12分
19、解:(1) 因为: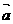 ={1, 2},
={1, 2},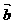 ={x,1},
={x,1},
所以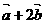 ={1+2x, 4},
={1+2x, 4},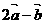 ={2–x, 3}……………………………………………2分
={2–x, 3}……………………………………………2分
又: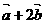 ∥
∥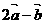 ,所以:
,所以: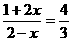 ,即:
,即: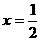 ,故
,故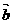 ={
={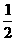 ,1}…………4分
,1}…………4分
(2) 设B (x, y
),则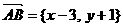 ;………………………………………………6分
;………………………………………………6分
由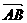 与
与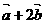 垂直得:
垂直得:
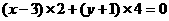 。…………………………………………………………8分
。…………………………………………………………8分
所以直线AB的一般式方程为:x+2y–1=0……………………………………………9分
18、证明:分别以AB、AD所在的直线为x轴和y轴,如图建立直角坐标系。………2分
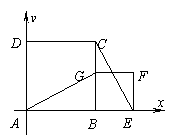 设AB=a,BE=b,
设AB=a,BE=b,
则A(0,0),G(a,b),E(a+b,0),C(a,a)…4分
kAG=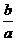 ,kEC= –
,kEC= –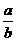 ,…………………………………6分
,…………………………………6分
因为kAG.kEC= –1,所以AG⊥CE。………………8分
注意:本题如果用向量方法来证,相应给分。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com