
题目列表(包括答案和解析)
9.设 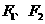 是双曲线
是双曲线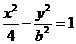 的两个焦点,点P在双曲线上,且
的两个焦点,点P在双曲线上,且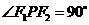 ,△
,△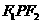 的面积为1,则正数b的值为
( )
的面积为1,则正数b的值为
( )
A.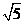 B.2
C.
B.2
C.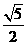 D.1
D.1
8.已知点A(1,2),过点(5,-2)且斜率为k的直线与抛物线y2=4x交于B、C两点,那么△ABC( )
A.是锐角三角形 B.是钝角三角形 C.是直角三角形 D.的形状与k值有关
7.直线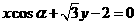 的倾斜角的范围是
( )
的倾斜角的范围是
( )
A.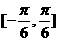 B.
B.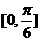 C.
C.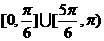 D.
D.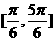
6.直线x-y-1=0与实轴在y轴上的双曲线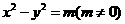 的交点在以原点为中心,边长为2且各边分别平行于坐标轴的正方形内部,则m的取值范围为
( )
的交点在以原点为中心,边长为2且各边分别平行于坐标轴的正方形内部,则m的取值范围为
( )
A.0<m<1 B.m<0 C.-1<m<0 D.m<-1
5.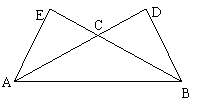 如图,在△ABC中,∠CAB=∠CBA=30°,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为
( )
如图,在△ABC中,∠CAB=∠CBA=30°,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为
( )
A.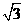 B.1 C.
B.1 C.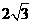 D.
D.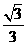
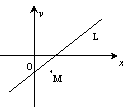
4.如图,已知点M(m,n)在直线l:Ax+By+C=0(AB≠0)的右下方,则Am+Bn+C的值 ( )
A.与A同号,与B同号 B.与A同号,与B异号
C.与A异号,与B异号 D.与A异号,与B同号
3.圆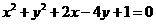 关于直线
关于直线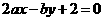 对称,则ab的最大值为 ( )
对称,则ab的最大值为 ( )
 A.1 B.
A.1 B.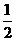 C.
C.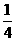 D.不存在
D.不存在
2.给出四个条件:①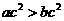 ;②
;②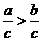 ;③
;③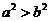 ;④
;④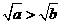 ,其中能分别成为a>b的充分条件的个数为
( )
,其中能分别成为a>b的充分条件的个数为
( )
A.0 B.1 C.2 D.3
1.抛物线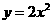 的准线方程为 ( )
的准线方程为 ( )
A.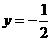 B.
B.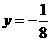 C.
C.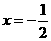 D.
D.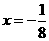
17 解关于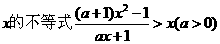 .
.
解: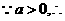 原不等式
原不等式 .
.
①当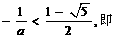
 ;
;
②当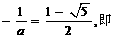
 ;
;
③当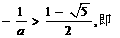

18 已知直线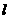 与椭圆
与椭圆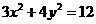 相交于
相交于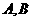 两点,弦
两点,弦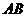 的中点坐标为
的中点坐标为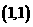 ,
,
求:⑴直线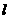 的方程;
⑵弦长
的方程;
⑵弦长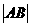 。
。
解:⑴设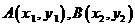 ,则有
,则有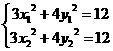
∴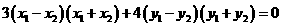 ∴
∴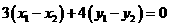
∴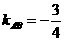 ∴
∴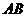 方程为
方程为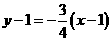 即
即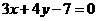 。
。
⑵由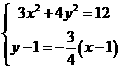 有
有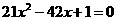 ∴
∴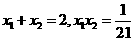
∴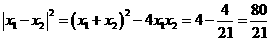
∴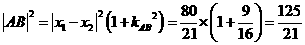 ∴
∴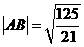
19 设直线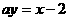 与抛物线
与抛物线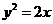 交于相异两点
交于相异两点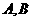 ,以线段
,以线段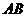 为直经作圆
为直经作圆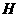 (
(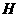 为圆心)。试证抛物线顶点在圆
为圆心)。试证抛物线顶点在圆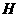 的圆周上;并求
的圆周上;并求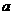 的值,使圆
的值,使圆 的面积最小。
的面积最小。
 解:设
解:设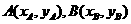 ,则其坐标满足
,则其坐标满足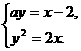
消去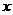 得:
得: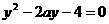 ,则
,则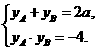
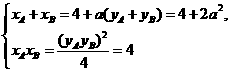
因此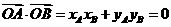 .
.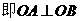 ,
,
故 必在圆
必在圆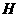 的圆周上。又由题意圆心
的圆周上。又由题意圆心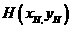 是
是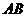 的中点,
的中点,
故 由前已证:
由前已证:
 应是圆
应是圆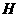 的半径,且
的半径,且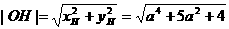 。
。
从而当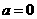 时,圆
时,圆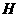 的半径最小,亦使圆
的半径最小,亦使圆 的面积最小.
的面积最小.
20 双曲线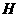 的渐近线方程为
的渐近线方程为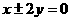 ,且
,且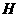 上动点
上动点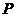 到定点
到定点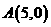 的最短距离为
的最短距离为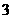 ,求双曲线
,求双曲线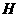 的方程。
的方程。
解:设双曲线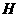 的方程为
的方程为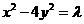 ,则
,则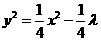 设
设
∴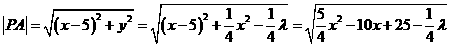
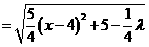
⑴当焦点在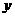 轴时,则有
轴时,则有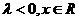 ,
,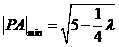 ,
,
∴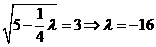 ,此时双曲线
,此时双曲线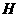 的方程
的方程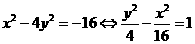
⑵当焦点在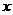 轴时,则有
轴时,则有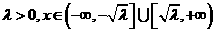 ,
,
①当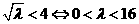 时,
时,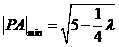 ∴
∴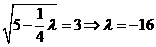 不合
不合
②当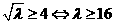 时,
时,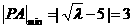
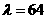
此时双曲线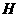 的方程
的方程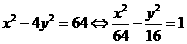
∴所求双曲线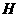 的方程
的方程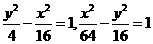 。
。
21
已知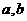 都是正数,
都是正数,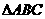 是平面直角坐标系
是平面直角坐标系 内,以两点
内,以两点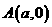 和
和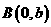 为顶点的正三角形,且它的第三个顶点
为顶点的正三角形,且它的第三个顶点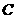 在第一象限内。
在第一象限内。
⑴若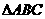 能含于正方形
能含于正方形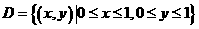 内, 试求:变量
内, 试求:变量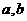 的约束条件,并在直角坐标系
的约束条件,并在直角坐标系 内画出约束条件表示的平面区域;
内画出约束条件表示的平面区域;
 ⑵当
⑵当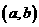 在⑴所得的约束条件内移动时,求
在⑴所得的约束条件内移动时,求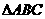 面积
面积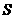 的最大值,并求此时
的最大值,并求此时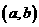 的坐标。
的坐标。
解: ⑴顶点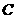 是以
是以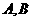 为圆心
为圆心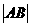 为半径的两圆在第一象限的交点,
为半径的两圆在第一象限的交点,
由圆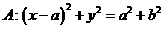 , 圆
, 圆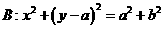 。
。
解得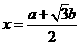 ,
,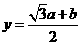 ,∴
,∴
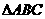 含于正方形
含于正方形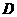 内,即三顶点
内,即三顶点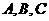 含于区域
含于区域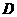 内时,
内时,
 ∴
∴ 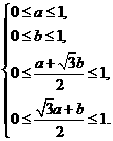
这就是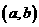 的约束条件。
的约束条件。
其图形为右图的六边形,∵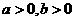 , ∴图中坐标轴上的点除外。
, ∴图中坐标轴上的点除外。
⑵∵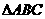 是边长为
是边长为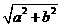 的正三角形,∴
的正三角形,∴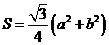
在⑴的条件下, 当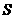 取最大值等价于六边形图形中的点
取最大值等价于六边形图形中的点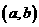 到原点的距离最大,
到原点的距离最大,
由六边形中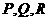 相应的
相应的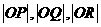 的计算:
的计算:
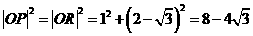 、
、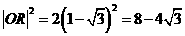 知:
知:
当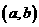 的坐标为
的坐标为 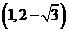 或
或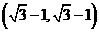 或
或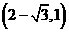 时,
时, 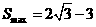 。
。
22
已知动点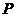 与双曲线
与双曲线 的两个焦点
的两个焦点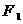 、
、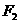 的距离之和为定值,
的距离之和为定值,
且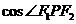 的最小值为
的最小值为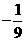 ,⑴求动点
,⑴求动点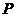 的轨迹方程;⑵若已知
的轨迹方程;⑵若已知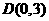 ,
,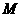 、
、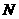 在动点
在动点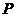 的轨迹上且
的轨迹上且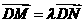 ,求实数
,求实数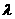 的取值范围.
的取值范围.
解:⑴由题意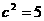 .设
.设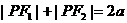 (
(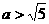 ),
),
由余弦定理得: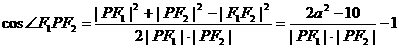 .
.
又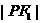 ·
·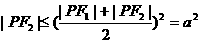 ,
,
当且仅当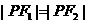 时,
时,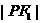 ·
·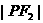 取最大值,
取最大值,
此时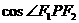 取最小值
取最小值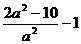 ,令
,令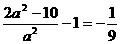 ,
,
解得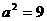 ,
,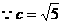 ,∴
,∴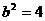 ,故所求
,故所求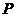 的轨迹方程为
的轨迹方程为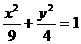 .
.
⑵设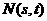 ,
,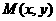 ,则由
,则由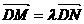 ,可得
,可得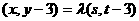 ,
,
故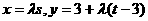 . ∵
. ∵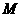 、
、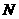 在动点
在动点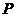 的轨迹上,
的轨迹上,

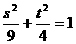 且
且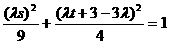 ,消去
,消去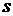 可得
可得
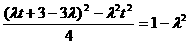 ,解得
,解得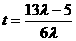 ,又
,又 ,∴
,∴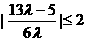 ,
,
解得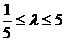 ,故实数
,故实数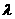 的取值范围是
的取值范围是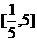 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com