22．(本小题满分10分)

设集合A=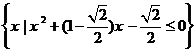，B=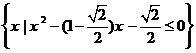，又设函数f(x)=2x²+mx-1.

(1)若不等式f(x)≤0的解集为C，且C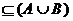，求实数m的取值范围；([-1,1]

(2)若对任意x∈R，都有f(1+x)=f(1-x)成立，当x∈(A∩B)时，试求f(x)的值域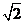；([-2,2])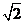

(3)(理科做)当m∈A∪B，x∈A∩B时，证明：|f(x)|≤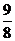(略)

21．(本小题满分8分)已知双曲线中心在原点，焦点在x轴上，离心率为2，F₁，F₂为左、右两个焦点，P是双曲线上的一点，若∠F₁PF₂=60⁰，△PF₁F₂的面积S△PF₁F₂=12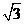，求双曲线的方程。()

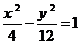20．(本小题满分8分)

　 (理科做)某种商品原来定价每件P元，每月将卖出n件，假设定价上涨x成(这里x成：即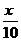，0<x≤10)，每月卖出数量将减少y成，而售货金额变成原来的S倍。设y=ax，其中满足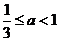的常数，用a表示当售货金额最大时x的值。

(售货金额最大时x=)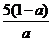

　(文科做)某种商品原来定价每件8元，每月将卖出100件，假设定价上涨x成(这里x成：即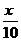，0<x≤10)，每月卖出数量将减少y成，而售货金额变成原来的S倍。设y=ax，其中满足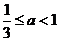的常数，用a表示当售货金额最大时x的值。(售货金额最大时x=)

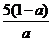19．(本小题满分10分)已知圆的方程(x+2)²+y²=1,求经过点P(-1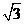，)的切线方程。

　 (x=-1和y=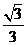x+)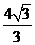

18．(本小题满分8分)设A₁，A₂椭圆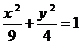的长轴的两个端点，P₁P₂是与A₁A₂垂直的弦，求直线A₁P₁与A₂P₂交点的轨迹方程。(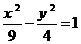(x≠±3))

17．(本小题满分8分)设不等式|2x+1|<-x与x²+ax+b<0同解，求a、b的值(a=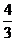,b=)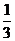

16、(理科做)过双曲线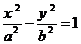(a>0，b>0)的左焦点且垂直于x轴的直线与双曲线相交于M、N两点，以MN为直径的圆恰好过双曲线右顶点，则双曲线的离心率等于_2_。

(文科做)已知|a|≠|b|，m=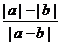,n=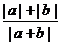，则m、n大小关系是__m≤n 。

15、中心在原点，准线方程为x=±4,离心率为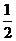的椭圆方程为。

14、已知x，y满足约束条件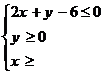，则z=2x+4y的最大值为24_。

13、设a、b∈R⁺,且a²+b²=a+b，那么a+b的最大值是__2__。