5．(习题二第16题)设点P(x0，y0)在直线As+By+C=0上，求证：这条直线的方程可以写成A(x-x0)+B(y-y0)=0．

证明：将点P(x0，y0)的坐标代入有C=-Ax0-By0，将C代入Ax+By+C=0即有A(x-x0)+B(y-y0)=0．

4．(习题二第十三题)求过点P(2，3)，并且在两轴上的截距相等的直线方程．

3．(习题二第8题)一条直线和y轴相交于点P(0，2)，它的倾斜角

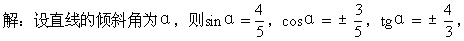
1．(1．6练习第1题)由下列条件，写出直线的方程，并化成一般式：

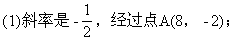
(2)经过点B(4，2)，平行于x轴；

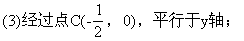
(5)经过两点P1(3，-2)、P2(5，-4)；

(6)x轴上的截距是-7，倾斜角是45°．

解：(1)x+2y-4=0；　 (2)y-2=0；　 (3)2x+1=0；

(4)2x-y-3=0；　 (5)x+y-1=0；　 (6)x-y+7=0．

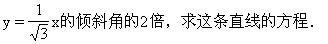
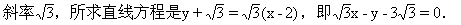
(四)课后小结

(1)归纳直线方程的五种形式及其特点．

(2)例4一般化：求过两点的直线与已知直线(或由线)的交点分以这两点为端点的有向线段所成定比时，可用定比分点公式设出交点的坐标，代入已知直线(或曲线)求得．

(三)例题

解：直线的点斜式是

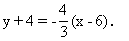
化成一般式得

4x+3y-12=0．

把常数次移到等号右边，再把方程两边都除以12，就得到截距式

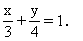
讲解这个例题时，要顺便解决好下面几个问题：(1)直线的点斜式、两点式方程由于给出的点可以是直线上的任意点，因此是不唯一的，一般不作为最后结果保留，须进一步化简；(2)直线方程的一般式也是不唯一的，因为方程的两边同乘以一个非零常数后得到的方程与原方程同解，一般方程可作为最终结果保留，但须化为各系数既无公约数也不是分数；(3)直线方程的斜截式与截距式如果存在的话是唯一的，如无特别要求，可作为最终结果保留．

例2　 把直线l的方程x-2y+6=0化成斜截式，求出直线l的斜率和在x轴与y轴上的截距，并画图．

解：将原方程移项，得2y=x+6，两边除以2得斜截式：

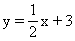
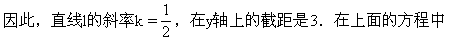
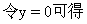
x=-6

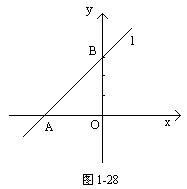
根据直线过点A(-6，0)、B(0，3)，在平面内作出这两点连直线就是所要作的图形(图1-28)．

本例题由学生完成，老师讲清下面的问题：二元一次方程的图形是直线，一条直线可由其方向和它上面的一点确定，也可由直线上的两点确定，利用前一点作图比较麻烦，通常我们是找出直线在两轴上的截距，然后在两轴上找出相应的点连线．

例3　 证明：三点A(1，3)、B(5，7)、C(10，12)在同一条直线上．

证法一　 直线AB的方程是：

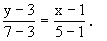
化简得　 y=x+2．

将点C的坐标代入上面的方程，等式成立．

∴A、B、C三点共线．

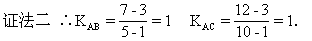
∴A、B、C三点共线．

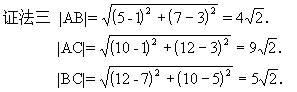
∵|AB|+|BC|=|AC|，

∴A、C、C三点共线．

讲解本例题可开拓学生思路，培养学生灵活运用知识解决问题的能力．

例4　 直线x+2y-10=0与过A(1，3)、　 B(5，2)的直线相交于C，

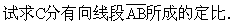
此题按常规解题思路可先用两点式求出AB的方程，然后解方程组得到点C的坐标，再求点C分AB所成的定比，计算量大了一些．如果先用定比分点公式设出点C的坐标(即满足点C在直线AB上)，然后代入已知的直线方程求λ，则计算量要小得多．

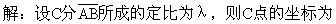
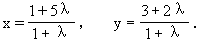
代入x+2y-10=0有：

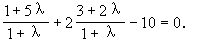
解之得　 λ=-3．

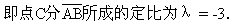
(二)直线方程的一般形式

我们知道，在直角坐标系中，每一条直线都有倾斜角α．当α≠90°时，直线有斜率，方程可写成下面的形式：

y=kx+b

当α=90°时，它的方程可以写成x=x0的形式．

由于是在坐标平面上讨论问题，上面两种情形得到的方程均可以看成是二元一次方程．这样，对于每一条直线都可以求得它的一个二元一次方程，就是说，直线的方程都可以写成关于x、y的一次方程．

反过来，对于x、y的一次方程的一般形式

Ax+By+C=0．　　　　　　　　　　　　　　　　　　　 (1)

其中A、B不同时为零．

(1)当B≠0时，方程(1)可化为

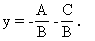
这里，我们借用了前一课y=kx+b表示直线的结论，不弄清这一点，会感到上面的论证不知所云．

(2)当B=0时，由于A、B不同时为零，必有A≠0，方程(1)可化为

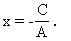
它表示一条与y轴平行的直线．

这样，我们又有：关于x和y的一次方程都表示一条直线．我们把方程写为

Ax+By+C=0

这个方程(其中A、B不全为零)叫做直线方程的一般式．

引导学生思考：直线与二元一次方程的对应是什么样的对应？

直线与二元一次方程是一对多的，同一条直线对应的多个二元一次方程是同解方程．

(一)引入新课

点斜式、斜截式不能表示与x轴垂直的直线；两点式不能表示与坐标轴平行的直线；截距式既不能表示与坐标轴平行的直线，又不能表示过原点的直线．与x轴垂直的直线可表示成x=x0，与x轴平行的直线可表示成y=y0。它们都是二元一次方程．

我们问：直线的方程都可以写成二元一次方程吗？反过来，二元一次方程都表示直线吗？

分析、启发、讲练结合．

3．疑点：直线与二元一次方程是一对多的关系．同条直线对应的多个二元一次方程是同解方程．