
题目列表(包括答案和解析)
7. 三个平面两两相交于三条直线,若这三条交线不互相平行,:求证它们必交于一点.
6.
已知直线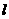 与三条平行直线
与三条平行直线 都相交,求证:这四条直线共面.
都相交,求证:这四条直线共面.
5. 不重合的三条直线,若相交于一点,则最多能确定 个平面; 若共有两个交点,最多能确定 个平面; 若共有三个交点,最多能确定 个平面.
4. 用适当的符号填空:若 则
则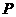
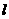 .
.
3.
两条相交直线 都在平面
都在平面 内且都不在平面
内且都不在平面 内. 命题甲:
内. 命题甲: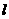 和
和 中至少有一条与
中至少有一条与 相交; 命题乙:平面
相交; 命题乙:平面 和
和 相交,则甲是乙的
( )
相交,则甲是乙的
( )
A.充分但不必要条件 B.必要但不充分条件
C.充分且必要条件 D.既非充分也非必要条件
2. 可使平面 和
和 重合的条件是它们的公共部分中有
( )
重合的条件是它们的公共部分中有
( )
A.三个点 B.一个点和一条直线
C.无数个点 D.两条不重合,不异面的直线
1. 下列判断正确的是 ( )
A.两条直线确定一个平面
B.如果平面 和
和 有三个公共点,则
有三个公共点,则 与
与 重合
重合
C.有一个公共点的两个平面交于过这一点的一条直线
D.点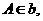 且
且 与平面
与平面 有公共点,则点
有公共点,则点 在平面
在平面 内
内
2.处理立体几何问题的基本思想是“降维”,把较为复杂的问题化归为平面几何问题(如例3).要充分利用平面几何中的基本图形解决问题.
[训练反馈]
1.会用图形语言、文字语言和符号语言准确描述三个公理(推论);理解它们的基本应用(如例1,例2).
3.证明三线 共点的主要方法有:①证明
共点的主要方法有:①证明 与
与 相交,
相交, 与
与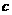 相交,再证交点重合;②先证
相交,再证交点重合;②先证 与
与 相交于点
相交于点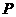 ,再证
,再证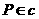 .
.
例2 已知四条直线 两两相交,但不共点,求证:
两两相交,但不共点,求证: 共面.
共面.
分析 四线不共点,三线有可能共点,也可能无三线共点,因而要分类讨论!
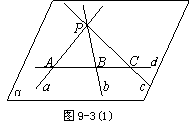
证明 ① 如图9-3(1),设 都经过点
都经过点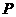 . 则由条件知此时
. 则由条件知此时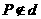 .
.
于是根据推论1,经过点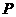 与直线
与直线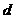 存在一个平面,设该平面为
存在一个平面,设该平面为 .
.
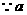 与
与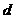 相交,设交点为
相交,设交点为 ,
,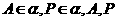 不是同一点,
不是同一点, .
.
同理 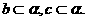 所以
所以 共面.
共面.
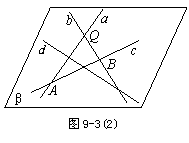
② 如图9-3(2),设无三条直线共点,由已知 相交,设交点为
相交,设交点为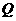 ,根据推论2,经过
,根据推论2,经过 存在一个平面,设该平面为
存在一个平面,设该平面为 .
.
 与
与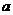 相交,
相交,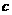 与
与 相交,且
相交,且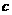 不经过点
不经过点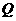 ,
, 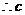 与
与 交于不同两点A,B,即
交于不同两点A,B,即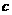 与平面
与平面 有两个不同的公共点,
有两个不同的公共点, 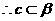 . 同理
. 同理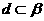 .所以
.所以 都在平面
都在平面 内,故
内,故 共面.
共面.
点评 证明共面问题的主要方法有:①先由公理3或其推论证明某些元素确定一个平面,再证其余元素都在此平面内; ② 指出给定的元素中的某些元素在平面 内,某些元素(与前述元素有公共元素,但两部分必须包括所有元素)在平面
内,某些元素(与前述元素有公共元素,但两部分必须包括所有元素)在平面 内,再通过公共元素来证明
内,再通过公共元素来证明 与
与 重合.如“若一直线与三条平行直线都相交,则这四条直线共面”的证明就用此法.
重合.如“若一直线与三条平行直线都相交,则这四条直线共面”的证明就用此法.
以上两例归纳了共线、共点、共面问题的证明思路。
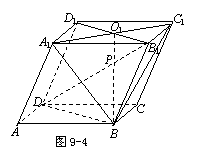 例3 如图9-4,平行六面体
例3 如图9-4,平行六面体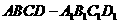 中,
中, 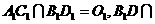 平面
平面 求证:
求证:
(1) 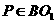 ;
;
(2) 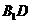 被平面
被平面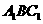 截于三等分点.
截于三等分点.
分析 (1) 要证点P在直线BO1上, 可考虑两个相交平面,
使点P为这两个平面的公共点,而BO1为这两个平面的交线.
(2)会用点、线、面去思维。
简证 (1) 因为点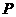 既在平面
既在平面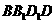 内,又在平面
内,又在平面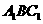 内,
内,
 所以
所以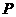 点必在它们的交线
点必在它们的交线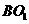 上. 从而
上. 从而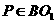 .
.
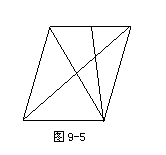
(2) 将对角面 移出(如图9-5),连
移出(如图9-5),连 (评:多余。其实由
(评:多余。其实由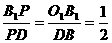 即得结论),
即得结论),
则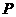 是△B1D1B的重心.
是△B1D1B的重心.
即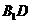 被平面
被平面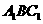 截于三等分点.
截于三等分点.
点评 将对角面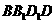 从线条复杂的平行六面体
从线条复杂的平行六面体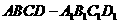 中移出,既使问题简单化,又将图形“恢复”其本来面目(平面图形).
分解和移动图形,“降维”等都是处理立体几何问题的重要思想方法.
中移出,既使问题简单化,又将图形“恢复”其本来面目(平面图形).
分解和移动图形,“降维”等都是处理立体几何问题的重要思想方法.
[知能集成]
本课的主要内容是平面的基本性质,它是研究立体几何的理论基础.
注意以下几点:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com