
题目列表(包括答案和解析)
3、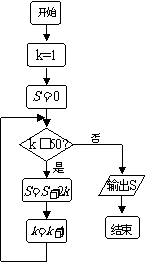 方程
方程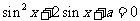 一定有解,则
一定有解,则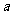 的取值范围是 ( )
的取值范围是 ( )
A.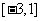 B.
B. C.
C. D. 以上都不对
D. 以上都不对
2、设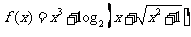 ,则对任意实数
,则对任意实数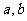 ,
,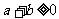 是
是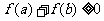 的( )
的( )
A. 充分必要条件 B. 充分而不必要条件
C. 必要而不充分条件 D. 既不充分也不必要条件
1、设集合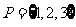 ,集合
,集合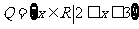 ,那么下列结论正确的是: ( )
,那么下列结论正确的是: ( )
A.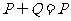 B.
B. 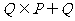 C.
C. 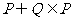 D.
D. 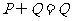
4.(本小题满分12分)假定某射手每次射击命中的概率为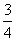 ,且只有
,且只有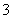 发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为
发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为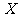 ,求:
,求:
⑴目标被击中的概率;
⑵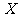 的概率分布;
的概率分布;
⑶均值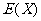 .
.
08届高考数学第二次诊断性考试试卷
3.(本小题满分10分)设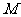 是把坐标平面上的点的横坐标伸长到
是把坐标平面上的点的横坐标伸长到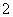 倍,纵坐标伸长到
倍,纵坐标伸长到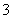 倍的伸压变换.
倍的伸压变换.
(1)求矩阵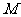 的特征值及相应的特征向量;
的特征值及相应的特征向量;
(2)求逆矩阵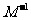 以及椭圆
以及椭圆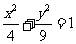 在
在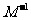 的作用下的新曲线的方程.
的作用下的新曲线的方程.
2.(本小题满分10分)求直线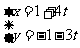 (
(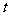 为参数)被曲线
为参数)被曲线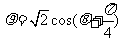 所截得的弦长.
所截得的弦长.
1.(本小题满分8分)求曲线 及直线
及直线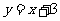 所围封闭区域的面积.
所围封闭区域的面积.
20.(本小题满分16分)定义在正整数集上的函数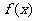 对任意
对任意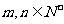 ,都有
,都有
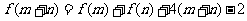 ,且
,且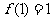 .
.
⑴求函数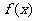 的表达式;
的表达式;
⑵若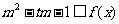 对于任意的
对于任意的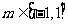 、
、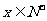 恒成立,求实数
恒成立,求实数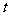 的取值范围;
的取值范围;
⑶对任意正整数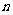 ,在
,在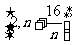 内总存在
内总存在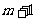 个实数
个实数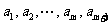 ,
,
使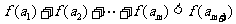 成立,求
成立,求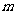 的最大值.
的最大值.
08届高考数学第二次诊断性考试试卷
数学附加题
19.(本小题满分16分)已知函数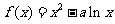 和
和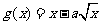 在
在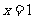 处的切线平行.
处的切线平行.
⑴试求函数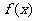 和
和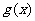 的单调增区间;
的单调增区间;
⑵设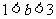 ,求证:
,求证: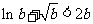 .
.
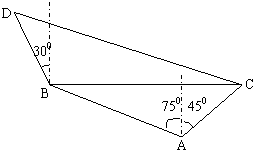
18.(本小题满分15分)在海岸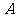 处,发现北偏西
处,发现北偏西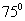 的方向,距离
的方向,距离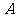
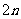 mile的
mile的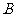 处有一艘走私船,在
处有一艘走私船,在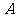 处北偏东
处北偏东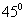 方向,距离
方向,距离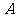
 mile的
mile的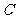 处的缉私船奉命以
处的缉私船奉命以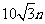 mile/h的速度追截走私船.此时,走私船正以
mile/h的速度追截走私船.此时,走私船正以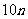 mile/h的速度从
mile/h的速度从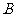 向北偏西
向北偏西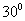 方向逃窜,问缉私船沿什么方向能最快追上走私船?
方向逃窜,问缉私船沿什么方向能最快追上走私船?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com