
题目列表(包括答案和解析)
13 过点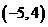 ,且在两坐标轴上截距相等的直线的方程为
,且在两坐标轴上截距相等的直线的方程为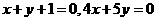 。
。
14 双曲线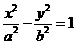 的一条准线被它的两条渐近线所截得线段长度恰好等于它的一个焦点到一条渐近线的距离,则该双曲线的离心率为 _2__ _。
的一条准线被它的两条渐近线所截得线段长度恰好等于它的一个焦点到一条渐近线的距离,则该双曲线的离心率为 _2__ _。
15 若方程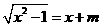 无解,则实数
无解,则实数 的取值范围是
的取值范围是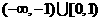 。
。
16 已知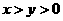 ,则
,则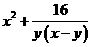 的最小值是_ _16_________。
的最小值是_ _16_________。
1 不等式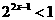 的解集是
( )
的解集是
( )
A 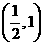 B
B
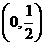 C
C
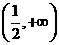 D
D 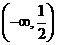
2 椭圆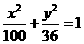 有一点
有一点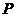 ,它到左准线的距离为10,那么
,它到左准线的距离为10,那么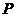 到右焦点的距离是( )
到右焦点的距离是( )
A 8 B 10 C 12 D 15
3 直线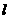 过点
过点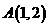 ,且
,且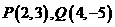 两点到直线
两点到直线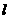 的距离相等,则
的距离相等,则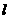 的方程为 ( )
的方程为 ( )
A 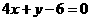 B
B
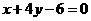
C 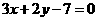 与
与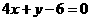 D
D 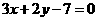 与
与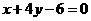
4 下列函数中最小值是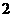 的函数是
( )
的函数是
( )
A 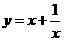 B
B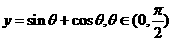 C
C 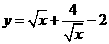 D
D 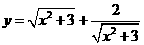
5 若直线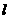 的倾斜角比直线
的倾斜角比直线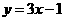 的倾斜角小
的倾斜角小 ,则直线
,则直线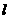 的斜率为
( )
的斜率为
( )
A 2
B 1 C 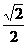 D
D 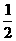
6 当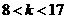 ,曲线
,曲线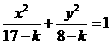 与
与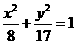 有相同的 ( )
有相同的 ( )
A 焦点 B 准线 C 焦距 D 离心率
7 设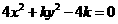 表示双曲线,则双曲线的虚轴长是 ( )
表示双曲线,则双曲线的虚轴长是 ( )
A 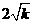 B
B 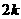 C
C 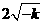 D
D 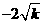
8 直线 与圆
与圆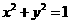 的位置关系一定是 ( )
的位置关系一定是 ( )
A 相离
B 相交
C 相切
D 与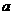 的取值有关
的取值有关
9 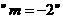 是“直线
是“直线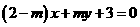 与直线
与直线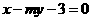 垂直”的 ( )
垂直”的 ( )
A 充分不必要条件 B 必要不充分条件 C 充要条件 D 不充分不必要条件
10、以椭圆两焦点为直径端点的圆交椭圆于不同的四点,顺次连接四个交点和两个焦点恰好围成一个正六边形,则这个椭圆的离心率为 ( )
A 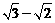 B
B
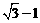 C
C
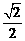 D
D
11 无论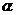 取何实数值,方程
取何实数值,方程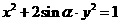 所表示的曲线必不是
( )
所表示的曲线必不是
( )
A 几条直线 B 圆 C 抛物线 D 双曲线
12 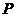 是抛物线
是抛物线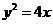 上一点,
上一点,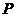 到
到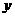 轴的距离为
轴的距离为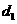 ,到直线
,到直线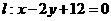 的距离为
的距离为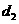 ,则
,则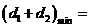 ( )
( )
A 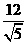 B
B
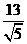 C
C
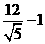 D
D
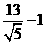
23.(本小题满分14分,前三小题满分各4分,第四小题满分2分)
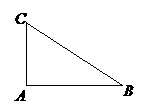
如图,在 中,
中,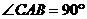 ,
,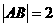 ,
,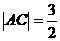 ,一曲线
,一曲线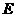 过点
过点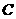 ,且曲线
,且曲线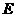 上任一点到
上任一点到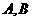 两点的距离之和不变.
两点的距离之和不变.
(1)建立适当的坐标系,求曲线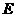 的方程;
的方程;
(2)设点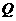 是曲线
是曲线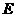 上的一动点,求线段
上的一动点,求线段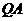 中点的轨迹方程;
中点的轨迹方程;
(3)设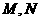 是曲线
是曲线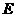 上不同的两点,直线
上不同的两点,直线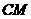 和
和 的倾斜角互补,试判断直线
的倾斜角互补,试判断直线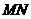 的斜率是否为定值。如果是,求这个定值;如果不是,请说明理由.
的斜率是否为定值。如果是,求这个定值;如果不是,请说明理由.
(4)若点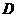 是曲线
是曲线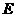 上的任一定点(除曲线
上的任一定点(除曲线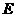 与直线
与直线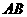 的交点),
的交点),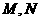 是曲线
是曲线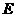 上不同的两点,直线
上不同的两点,直线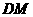 和
和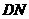 的倾斜角互补,直线
的倾斜角互补,直线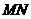 的斜率是否为定值呢?如果是,请你指出这个定值。(本小题不必写出解答过程)
的斜率是否为定值呢?如果是,请你指出这个定值。(本小题不必写出解答过程)
江苏省前黄高中2005~2006年度高二年级上学期期末考试
22.(本小题满分14分,第一小题满分6分,第二小题满分8分)
已知双曲线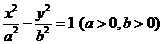 的右焦点为
的右焦点为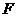 ,过点
,过点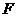 作直线
作直线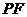 垂直于该双曲线的一条渐近线
垂直于该双曲线的一条渐近线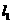 于
于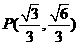 .
.
(1)求该双曲线的方程;
(2)过点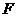 作直线
作直线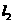 交该双曲线于
交该双曲线于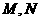 两点,如果
两点,如果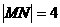 ,求直线
,求直线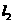 的方程.
的方程.
21. (本小题满分14分,第一小题满分4分,第二、第三小题满分各5分)
(本小题满分14分,第一小题满分4分,第二、第三小题满分各5分)
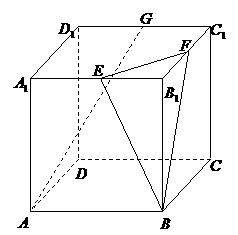
如图,在棱长为1的正方体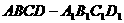 中,
中,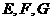 分别为
分别为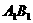 、
、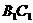 、
、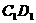 的中点.
的中点.
(1)求异面直线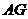 与
与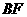 所成角的余弦值;
所成角的余弦值;
(2)求证: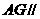 平面
平面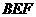 ;
;
(3)试在棱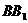 上找一点
上找一点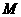 ,使
,使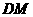 ⊥平面
⊥平面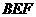 ,并证明你的结论.
,并证明你的结论.
20. (本小题满分12分,每小题满分6分)
(本小题满分12分,每小题满分6分)
如图,已知边长都为1正方形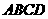 与正方形
与正方形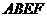 ,
,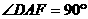 ,
,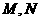 分别是对角线
分别是对角线 和
和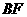 上的点,且
上的点,且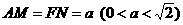 .
.
(1)求证: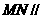 平面
平面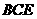 ;
;
(2)求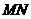 的最小值.
的最小值.
19.(本小题满分12分,每小题满分6分)
已知圆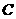 :
: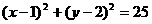 ,直线
,直线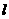 :
: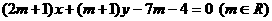 .
.
(1)求证:不论 取何实数,直线
取何实数,直线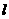 恒过一个定点;
恒过一个定点;
(2)求直线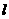 被圆
被圆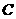 截得的弦长最小时,直线
截得的弦长最小时,直线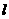 的方程.
的方程.
17. 18.
15. 16.
13. 14.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com