
题目列表(包括答案和解析)
20.(本题满分12分)
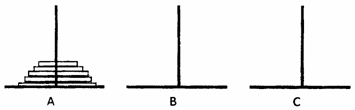 汉诺塔问题是根据一个传说形成的一个问题:有三根杆子和套在一根杆子上的若干大小不等的穿孔圆盘,按下列规则,把圆盘从一根杆子上全部移到另一根杆子上.
汉诺塔问题是根据一个传说形成的一个问题:有三根杆子和套在一根杆子上的若干大小不等的穿孔圆盘,按下列规则,把圆盘从一根杆子上全部移到另一根杆子上.
①每次只能移动1个碟片;②大盘不能叠在小盘上面.
如图所示,将A杆上所有碟片移到C杆上,B杆可以作为过渡杆使用,称将碟片从一个杆子移动到另一个标子为移动一次,记将A杆子上的n个碟片移动到C杆上最少需要移动an次.
(Ⅰ)写出a1,a2,a3,a4的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设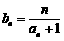 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
19. (本题满分12分)
(本题满分12分)
为迎接建党90周年,某班开展了一次“党史知识竞赛”,竞赛分初赛和决赛两个阶段进行,在初赛后,把成绩(满分为100分,分数均匀整数)进行统计,制成如右图的频率分布表:
(Ⅰ)求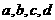 的值;
的值;
(Ⅱ)决赛规则如下:为每位参加决赛的选手准备四道题目,选手对其依次作答,答对两道就终止答题,并获得一等奖,若题目答完仍然只答对一道,则获得二等奖.
某同学进入决赛,每道题答对的概率P的值恰好与频率分布表中不少于90分的频率的值相同.设该同学决赛中答题个数为X,求X的分布列以及X的数学期望.
18. (本题满分12分)
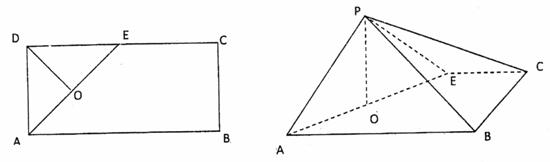
如图所示,在矩形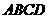 中,
中,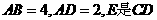 的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且
的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且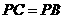 .
.
(Ⅰ)求证: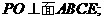
(Ⅱ)求二面角E-AP-B的余弦值.
17. (本题满分12分)已知函数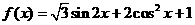
(Ⅰ)求函数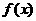 的单调递增区间;
的单调递增区间;
(Ⅱ)设△ABC的内角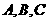 对边分别为
对边分别为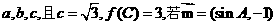 与
与
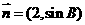 垂直,求
垂直,求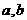 的值.
的值.
16.在实数集R中定义一种运算“△”,且对任意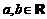 ,具有性质:
,具有性质:
①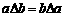 ; ②
; ②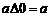 ;
;
③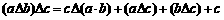 ,
,
则函数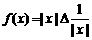 的最小值为
.
的最小值为
.
15.已知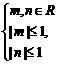 则在方程
则在方程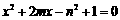
有实数根的条件下,又满足m≥n的概率为
14.若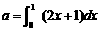 ,则二项式(
,则二项式(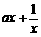 )6的展开式中的常数项为
)6的展开式中的常数项为
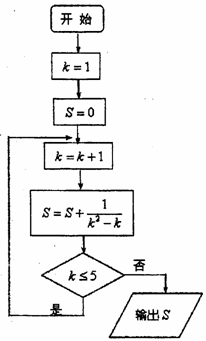
13.按右图所示的程序框图运算,则输出S的值是 .
12.已知函数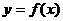 的定义域是R,若对于任意的正数a,函数g(x)=f(x)-f(x-a)都是其定义域上
的定义域是R,若对于任意的正数a,函数g(x)=f(x)-f(x-a)都是其定义域上
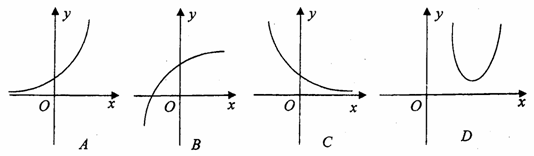 的减函数,则函数
的减函数,则函数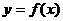 的图象可能是( )
的图象可能是( )
第Ⅱ卷(非选择题,共90分)
11.已知两点A(1,0),B(1,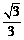 ),O为坐标原点,点C在第三象限,且
),O为坐标原点,点C在第三象限,且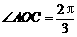 ,设
,设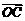 =2
=2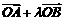 ,则
,则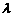 等于
( )
等于
( )
A.-2 B.2 C.-3 D.3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com