
题目列表(包括答案和解析)
1.已知集合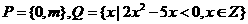 ,若
,若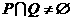 ,则
,则 等于
等于
A.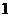 B.
B.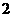 C.
C.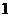 或
或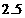 D.
D.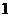 或
或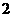
21. (本小题满分14分)
已知函数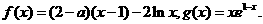 (
(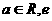 为自然对数的底数)
为自然对数的底数)
(1)当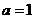 时,求
时,求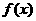 的单调区间;
的单调区间;
(2)若函数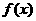 在
在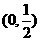 上无零点,求
上无零点,求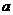 的最小值;
的最小值;
(3)若对任意给定的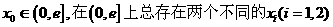 ,使得
,使得
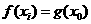 成立,求
成立,求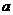 的取值范围。
的取值范围。
20. (本小题满分13分)
(本小题满分13分)
如图所示,椭圆C: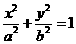
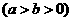 的一个焦点
的一个焦点
为 F(1,0),且过点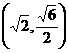 。
。
(1)求椭圆C的方程;
(2)已知A、B为椭圆上的点,且直线AB垂直于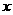 轴,
轴,
直线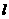 :
: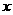 =4与
=4与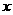 轴交于点N,直线AF与BN交
轴交于点N,直线AF与BN交
于点M。
(ⅰ)求证:点M恒在椭圆C上;
(ⅱ)求△AMN面积的最大值.
19. (本小题满分12分)
已知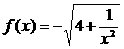 ,数列
,数列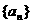 的前n项和为
的前n项和为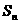 ,点
,点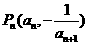 在曲线
在曲线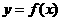 上
上
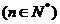 ,且
,且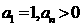 。
。
(1)求数列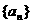 的通项公式;
的通项公式;
(2)数列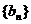 的前n项和为
的前n项和为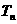 ,且满足
,且满足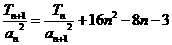 ,
,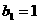 ,求数列
,求数列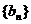 的通项公式;
的通项公式;
(3)求证: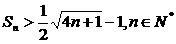 .
.
18.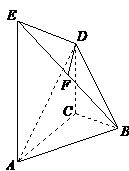 (本小题满分12分)
(本小题满分12分)
在如图所示的几何体中,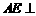 平面
平面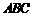 ,
, ∥
∥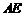 ,
,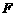 是
是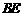 的
的
中点,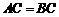
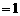 ,
,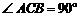 ,
,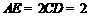 .
.
(1)证明 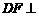 平面
平面 ;
;
(2)求二面角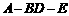 的余弦值的大小;
的余弦值的大小;
17. (本小题满分12分)
为了降低能源损耗,鹰潭市室内体育馆的外墙需要建造隔热层.体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度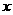 (单位:cm)满足关系:
(单位:cm)满足关系: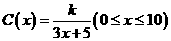 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设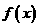 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求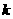 的值及
的值及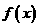 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用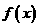 达到最小,并求最小值.
达到最小,并求最小值.
16.(本小题满分12分)
在△ABC中,内角A,B,C所对边长分别为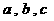 ,
,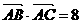 ,
,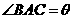 ,
,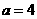 .
.
(1)求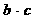 的最大值及
的最大值及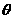 的取值范围;
的取值范围;
(2)求函数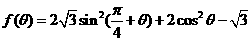 的最值.
的最值.
15. (考生注意:请在下列二题中任选一题作答,如果多做,则按所做的第一题评阅记分.)
(A)(选修4-4坐标系与参数方程)曲线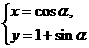 (
(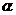 为参数)与曲线
为参数)与曲线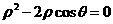 的交点个数为
个.
的交点个数为
个.
(B)(选修4-5不等式选讲)若不等式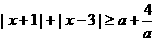 对任意的实数
对任意的实数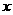 恒成立,则实数
恒成立,则实数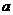 的取值范围是
.
的取值范围是
.
14. 设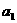 ,
,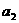 ,…,
,…,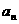 是1,2,…,
是1,2,…,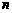 的一个排列,把排在
的一个排列,把排在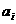 的左边且比
的左边且比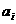 小的数的个数称为
小的数的个数称为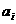 的顺序数(
的顺序数(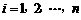 ).如在排列6,4,5,3,2,1中,5的顺序数为1,3的顺序数为0.则在由1、2、3、4、5、6、7、8这八个数字构成的全排列中,同时满足8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列的种数为_________ ___(结果用数字表示).
).如在排列6,4,5,3,2,1中,5的顺序数为1,3的顺序数为0.则在由1、2、3、4、5、6、7、8这八个数字构成的全排列中,同时满足8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列的种数为_________ ___(结果用数字表示).
13. 函数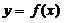
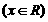 ,满足:对任意的x
,满足:对任意的x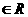 ,都有
,都有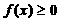 且
且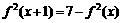 。当
。当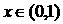 时,
时,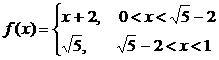 ,则
,则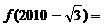 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com