
题目列表(包括答案和解析)
13、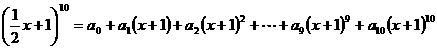 ,其中
,其中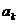 (
(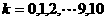 )都是常数,则
)都是常数,则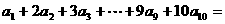 __________.
__________.
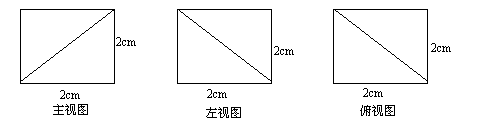
12、已知一个棱长为2cm的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的表面积为 .

11、等比数列{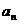 }中,
}中,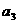 =6,前三项和
=6,前三项和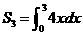 ,则公比q的值为
.
,则公比q的值为
.
21.(本题满分14分)
已知函数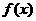 =
=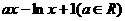 ,
,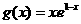 .
.
(1)求函数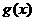 在区间
在区间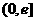 上的值域;
上的值域;
(2)是否存在实数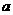 ,对任意给定的
,对任意给定的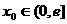 ,在区间
,在区间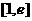 上都存在两个不同的
上都存在两个不同的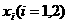 ,使得
,使得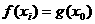 成立.若存在,求出
成立.若存在,求出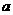 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(3)给出如下定义:对于函数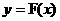 图象上任意不同的两点
图象上任意不同的两点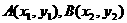 ,如果对于函数
,如果对于函数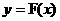 图象上的点
图象上的点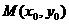 (其中
(其中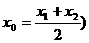 总能使得
总能使得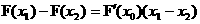 成立,则称函数具备性质“
成立,则称函数具备性质“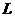 ”,试判断函数
”,试判断函数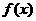 是不是具备性质“
是不是具备性质“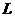 ”,并说明理由.
”,并说明理由.
20.(本题满分13分)
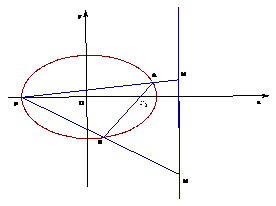
如图,已知 是椭圆
是椭圆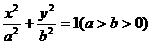 上的一个动点,
上的一个动点,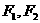 分别为椭圆的左、右焦点,弦
分别为椭圆的左、右焦点,弦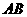 过点
过点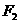 ,当
,当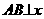 轴时,恰好有
轴时,恰好有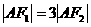 .
.
(1)求椭圆的离心率;
(2)设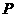 是椭圆的左顶点,
是椭圆的左顶点,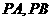 分别与椭圆右准线交与
分别与椭圆右准线交与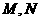 两点,求证:以
两点,求证:以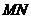 为直径的圆
为直径的圆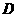 一定经过一定点,并求出定点坐标.
一定经过一定点,并求出定点坐标.
19、(本题满分12分)
已知数列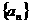 满足
满足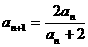 (
(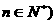 ,
,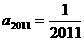 .
.
(1)求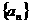 的通项公式;
的通项公式;
(2) 若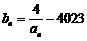 且
且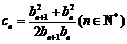 ,求证:
,求证: 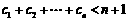 .
.
18、(本题满分12分)
在斜三棱柱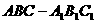 中,侧面
中,侧面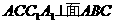 ,
,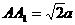 ,
,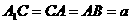 ,
,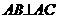 ,
,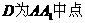 .
.
(1)求证: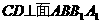 ;
;
(2)在侧棱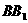 上确定一点
上确定一点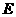 ,使得二面角
,使得二面角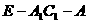 的大小为
的大小为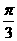 .
.
17、(本题满分12分)
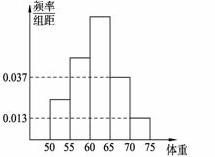
为了解今年某校高三毕业班准备报考飞行员学生的体重情
况,将所得的数据整理后,画出了频率分布直方图(如图),
已知图中从左到右的前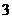 个小组的频率之比为
个小组的频率之比为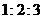 ,其中第
,其中第
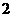 小组的频数为
小组的频数为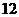 .
.
(1)求该校报考飞行员的总人数;
(2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中(人数很多)任选三人,设X表示体重超过60公斤的学生人数,求X的分布列和数学期望.

16、(本题满分12分)
在△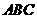 中,角
中,角 ,
,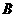 ,
,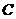 的对边分别为
的对边分别为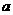 ,
,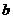 ,
,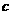 ,且满足
,且满足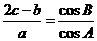 .
.
(1)求角 的大小;
的大小;
(2)若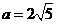 ,求△
,求△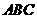 面积的最大值.
面积的最大值.
15、选做题(考生注意:请在(A)(B)两题中,任选做一题作答,若多做,则按(A)题计分)
(A)(参数方程与极坐标选讲)已知在极坐标系下,点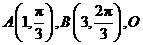 是极点,则
是极点,则 的面积等于_______;
的面积等于_______;
(B)关于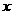 的不等式
的不等式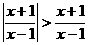 的解集是____ ____.
的解集是____ ____.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com