
题目列表(包括答案和解析)
5.各项都是正数的等比数列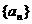 中,且
中,且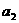 、
、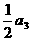 、
、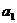 成等差数列,
成等差数列,
则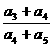 的值为( )
的值为( )
A.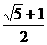 B.
B.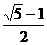 C.
C.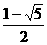 D.
D.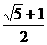 或
或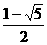
4.设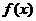 表示
表示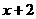 与
与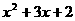 中的较大者,则
中的较大者,则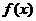 的最小值为( )
的最小值为( )
A.0 B.2 C.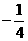 D.不存在
D.不存在
3. 若函数
若函数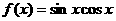 ,下列结论中正确的是( )
,下列结论中正确的是( )
A. 函数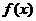 为偶函数
B.函数
为偶函数
B.函数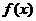 最小正周期为
最小正周期为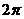
C. 函数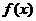 的图象关于原点对称 D.函数
的图象关于原点对称 D.函数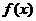 的最大值为
的最大值为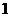
2.设集合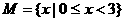 ,
,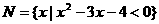 ,则集合
,则集合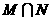 等于( )
等于( )
A.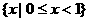 B.
B. 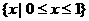 C.
C. 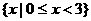 D.
D.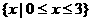
1.复数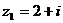 ,
,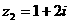 ,则
,则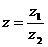 在复平面内对应点位于( )
在复平面内对应点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
21.(本小题满分14分)
已知函数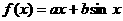 ,当
,当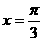 时,
时,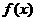 取得极小值
取得极小值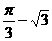 .
.
(1)求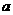 ,
,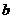 的值;
的值;
(2)设直线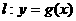 ,曲线
,曲线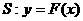 .若直线与曲线
.若直线与曲线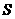 同时满足下列两个条件:
同时满足下列两个条件:
①直线与曲线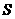 相切且至少有两个切点;
相切且至少有两个切点;
②对任意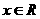 都有
都有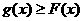 .则称直线为曲线
.则称直线为曲线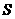 的“上夹线”.
的“上夹线”.
试证明:直线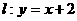 是曲线
是曲线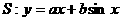 的“上夹线”.
的“上夹线”.
(3)记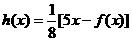 ,设
,设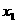 是方程
是方程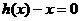 的实数根,若对于
的实数根,若对于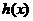 定义域中任意的
定义域中任意的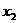 、
、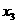 ,当
,当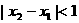 ,且
,且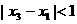 时,问是否存在一个最小的正整数
时,问是否存在一个最小的正整数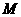 ,使得
,使得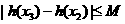 恒成立,若存在请求出
恒成立,若存在请求出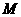 的值;若不存在请说明理由.
的值;若不存在请说明理由.
20.(本小题满分13分)
已知抛物线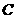 :
: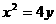 的焦点为
的焦点为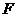 ,过点
,过点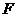 作直线交抛物线
作直线交抛物线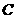 于
于 、
、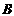 两点;椭圆
两点;椭圆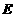 的中心在原点,焦点在
的中心在原点,焦点在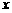 轴上,点
轴上,点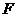 是它的一个顶点,且其离心率
是它的一个顶点,且其离心率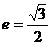 .
.
(1)求椭圆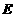 的方程;
的方程;
(2)经过 、
、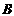 两点分别作抛物线
两点分别作抛物线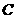 的切线
的切线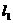 、
、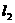 ,切线
,切线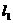 与
与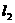 相交于点
相交于点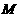 .证明:
.证明: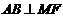 ;
;
(3) 椭圆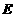 上是否存在一点
上是否存在一点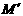 ,经过点
,经过点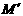 作抛物线
作抛物线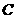 的两条切线
的两条切线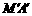 、
、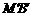 (
( 、
、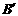 为切点),使得直线
为切点),使得直线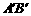 过点
过点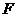 ?若存在,求出抛物线
?若存在,求出抛物线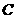 与切线
与切线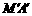 、
、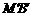 所围成图形的面积;若不存在,试说明理由.
所围成图形的面积;若不存在,试说明理由.
19.(本小题满分12分)
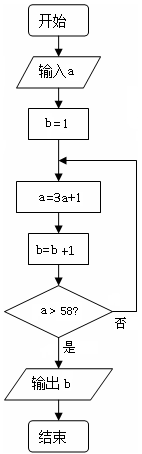
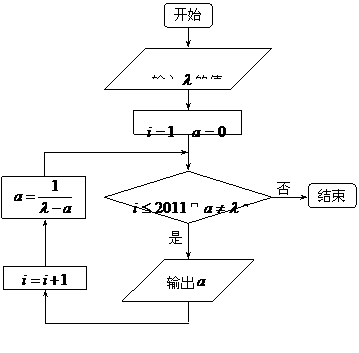 执行下面框图所描述的算法程序,记输出的一列数依次为
执行下面框图所描述的算法程序,记输出的一列数依次为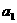 ,
,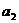 ,…,
,…,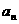 ,
,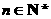 ,
,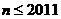 .
.
(1)若输入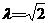 ,写出输出结果;
,写出输出结果;
(2)若输入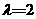 ,求数列
,求数列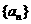 的通项公式;
的通项公式;
(3)若输入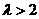 ,令
,令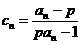 ,
,
求常数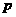 (
(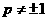 ),使得
),使得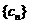 是等比数列.
是等比数列.
18.(本小题满分12分)
一个几何体是由圆柱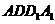 和三棱锥
和三棱锥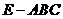 组合而成,点
组合而成,点 、
、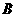 、
、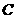 在圆
在圆 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图所示,其中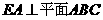 ,
,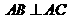 ,
,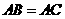 ,
,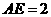 .
.
(1)求证: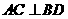 ;
;
(2)求二面角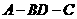 的平面角的大小.
的平面角的大小.

17.(本小题满分12分)
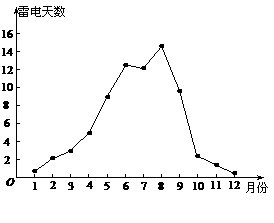
为了评估天气对大运会的影响,制定相应预案,深圳市气象局通过对最近50多年的气象数据资料的统计分析,发现8月份是本市雷电天气高峰期,在31天中平均发生雷电14.57天如图.如果用频率作为概率的估计值,并假定每一天发生雷电的概率均相等,且相互独立.
(1)求在大运会开幕(8月12日)后的前3天比赛中,恰好有2天发生雷电天气的概率(精确到0.01);
 (2)设大运会期间(8月12日至23日,共12天),发生雷电天气的天数为
(2)设大运会期间(8月12日至23日,共12天),发生雷电天气的天数为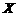 ,求
,求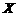 的数学期望和方差.
的数学期望和方差.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com