
题目列表(包括答案和解析)
1. 已知集合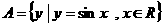 ,集合
,集合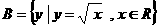 ,则
,则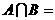 .
.
3、投掷四枚不同的金属硬币A、B、C、D,假定A、B两枚正面向上的概率均为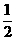 ,另两枚C、D为非均匀硬币,正面向上的概率均为a(0<a<1),把这四枚硬币各投掷一次,设孜表示正面向上的枚数.
,另两枚C、D为非均匀硬币,正面向上的概率均为a(0<a<1),把这四枚硬币各投掷一次,设孜表示正面向上的枚数.
(1)若A、B出现一正一反与C、D出现两正的概率相等,求a的值;
(2)求孜的分布列及数学期望(用a表示);
(3)若出现2枚硬币正面向上的概率最大,试求a的取值范围.
解:(Ⅰ)由题意,得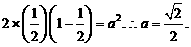 ………………………………2分
………………………………2分
(Ⅱ)着=0,1,2,3,4.
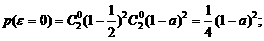 ………………………………………………3分
………………………………………………3分
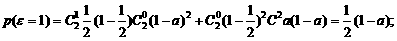 ……………………4分
……………………4分
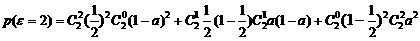
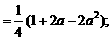 ………………………………………………………………5分
………………………………………………………………5分
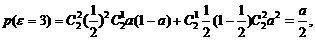 …………………………………6分
…………………………………6分
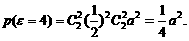 …………………………………………………………7分
…………………………………………………………7分
得孜的分布列为:
|
孜 |
0 |
1 |
2 |
3 |
4 |
|
p |
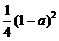 |
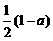 |
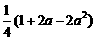 |
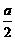 |
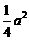 |
孜的数学期望为:
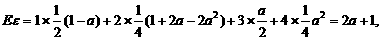 ……………………8分
……………………8分
(Ⅲ)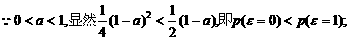 …………………9分
…………………9分
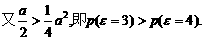 …………………………………………………10分
…………………………………………………10分
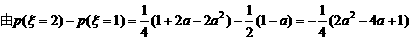 ≥0 .
≥0 .
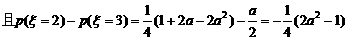 ≥0 . ………………11分
≥0 . ………………11分
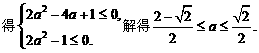
 ……………………………………………………12分
……………………………………………………12分
2、已知圆的极坐标方程为: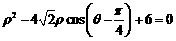 .
.
⑴将极坐标方程化为普通方程;
⑵若点P(x,y)在该圆上,求x+y的最大值和最小值.
1、变换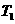 是逆时针旋转
是逆时针旋转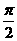 的旋转变换,对应的变换矩阵是
的旋转变换,对应的变换矩阵是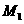 ;变换
;变换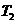 对应用的变换矩阵是
对应用的变换矩阵是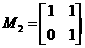 .
.
(Ⅰ)求点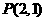 在
在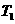 作用下的点
作用下的点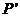 的坐标;
的坐标;
(Ⅱ)求函数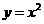 的图象依次在
的图象依次在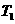 ,
,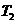 变换的作用下所得曲线的方程.
变换的作用下所得曲线的方程.
解:(Ⅰ)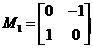 ,
,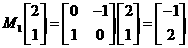 所以点
所以点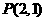 在
在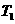 作用下的点
作用下的点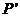 的坐标是
的坐标是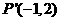 。(Ⅱ)
。(Ⅱ)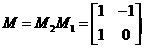 ,设
,设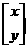 是变换后图像上任一点,与之对应的变换前的点是
是变换后图像上任一点,与之对应的变换前的点是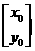 /则
/则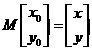 ,也就是
,也就是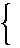
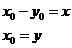 ,即
,即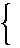
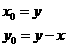 ,所以,所求曲线的方程是
,所以,所求曲线的方程是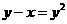 。
。
18、已知函数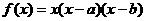 ,点
,点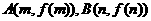 .
.
(1)设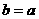 ,求函数
,求函数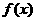 的单调区间;
的单调区间;
(2)若函数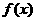 的导函数
的导函数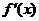 满足:当
满足:当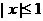 时,有
时,有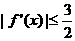 恒成立,求函数
恒成立,求函数
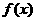 的表达式;
的表达式;
(3)若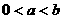 ,函数
,函数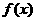 在
在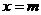 和
和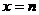 处取得极值,且
处取得极值,且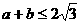 .问:是否存在常数
.问:是否存在常数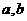 ,使得
,使得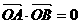 ? 若存在,求出
? 若存在,求出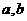 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)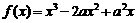 令
令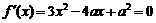 , 得:
, 得: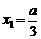 ,
,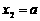 .
.
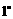 当
当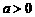 时,
时, 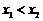
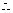 所求单调增区间是
所求单调增区间是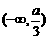 ,
,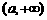 , 单调减区间是(
, 单调减区间是(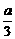 ,
,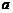 )
)
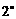 当
当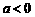 时,所求单调增区间是
时,所求单调增区间是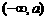 ,
,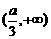 , 单调减区间是(
, 单调减区间是(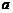 ,
,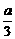 )
)
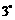 当
当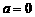 时,
时,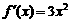 ≥
≥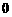 所求单调增区间是
所求单调增区间是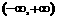 .
.
(2)
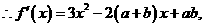
 当
当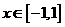 时,恒有
时,恒有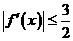
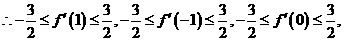
即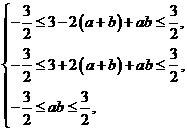 得
得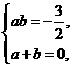
此时,满足当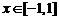 时
时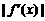 ≤
≤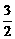 恒成立.
恒成立.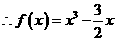 .
.
(3)存在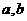 使得
使得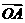
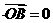 .
.
若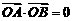 ,即
,即

由于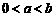 ,知
,知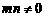
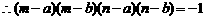 1
1
由题设,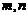 是
是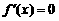 的两根
的两根
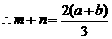 ,
,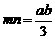 2
2
2代入1得: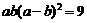
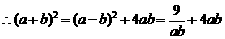 ≥
≥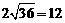 ,当且仅当
,当且仅当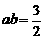 时取“=”
时取“=” 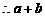 ≥
≥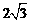
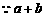 ≤
≤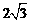
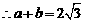 又
又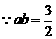 ,
,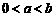
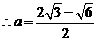 ,
, 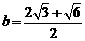 .
.
附加题
17、已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.
(1)求曲线C的方程;
(2)设n是过原点的直线,l是与n垂直相交于点P,且与曲线C相交于A、B两点的直线,且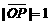 ,问:是否存在上述直线l使
,问:是否存在上述直线l使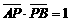 成立?若存在,求出直线l的方程,若不存在,请说明理由
成立?若存在,求出直线l的方程,若不存在,请说明理由
解:(Ⅰ)设M(x,y)是曲线C上任意一点,那么点M(x,y)满足
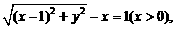
化简,得y2=4x(x>0). ………………………………………………………………………3分
注:(1)未写x>0的不扣分;
(2)由抛物线的定义直接得方程,只要设出方程y2=2px.说明p=2,也可得3分.
(Ⅱ)设A,B两点的坐标分别为(x1,y1),(x2,y2).
假设使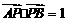 成立的直线l存在.
成立的直线l存在.
①当l不垂直于x轴时,设l的方程为y=kx+m,
由l与n垂直相交于P点且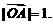 得
得
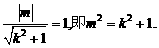 ①……………………………………………………………4分
①……………………………………………………………4分
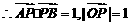
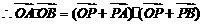 …………………………………………………………5分
…………………………………………………………5分
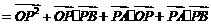
=1+0+0-1=0,即x1x2+ y1y2=0. ……………………………………………………6分
将y=kx+m代入方程y2=4x,得k2x2+(2km-4)x+m2=0. ………………………………………7分
∵l与C有两个交点,∴k≠0,
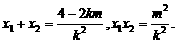 ②
②
∴x1x2+y1y2=x1x2+(kx1+m) (kx2+m)
=(1+k2)x1x2+km (x1+x2)+ m2=0. ③……………………………………………8分
将②代入③得
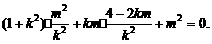
化简,得m2+4km=0. ……………………………………………………………………9分
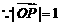 ∴m≠0 ① ∴m+4k=0 ④
∴m≠0 ① ∴m+4k=0 ④
由①、④得
 …………………………………………………10分
…………………………………………………10分
得存在两条直线l满足条件,其方程为: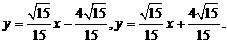
②当l垂直于x轴时,则n为x轴,P点坐标为(1,0),A(1,2),B(1,-2).

综上,符合题意的直线l有两条: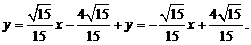 ………12分
………12分
注:第Ⅱ问设l的方程为x=ly+m,联立y2=4x建立y的一元二次方程更简单,且不需讨论.
16、将数列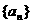 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表:
将数列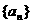 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表:
a1
a2,a 3
a 4,a 5,a 6
a7,a8,a9,a10
……
记表中的第一列数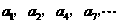 构成的数列为
构成的数列为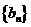 ,
,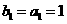 .
.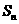 为数列
为数列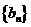 的前
的前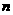 项和,且满足
项和,且满足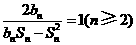 .
.
(Ⅰ)证明数列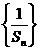 成等差数列,并求数列
成等差数列,并求数列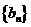 的通项公式;
的通项公式;
(Ⅱ)上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当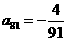 时,求上表中第
时,求上表中第 行所有项的和.
行所有项的和.
证明:(Ⅰ)由已知 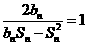 ,又
,又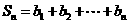 ,所以
,所以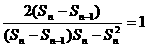 ,
,
即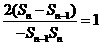 ,所以
,所以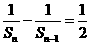
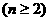 , 又
, 又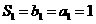 .
.
所以数列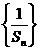 是首项为1,公差为
是首项为1,公差为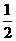 的等差数列.由上式可知
的等差数列.由上式可知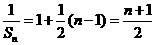 ,即
,即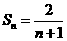 . 所以当
. 所以当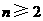 时,
时,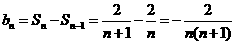 .
.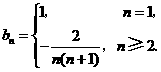
(Ⅱ)解:设上表中从第三行起,每行的公比都为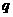 ,且
,且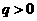 .因为
.因为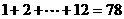 ,
,
所以表中第1行至第12行共含有数列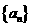 的前78项,故
的前78项,故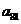 在表中第13行第三列,
在表中第13行第三列,
因此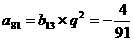 又
又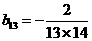 ,所以
,所以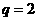 . 记表中第
. 记表中第 行所有项的和为
行所有项的和为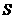 ,
,
则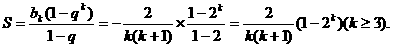
15、在△ABC中,a,b,c分别为内角A、B、C的对边,且2asinA=(2b-c)sinB+(2c-b)sinC.
(Ⅰ)求角A的大小;
(Ⅱ)若sinB+sinC=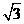 ,试判断△ABC的形状。
,试判断△ABC的形状。
解:(Ⅰ)由2asinA=(2b-c)sinB+(2c-b)sinC,
得2a2=(2b-c)b+(2c-b)c,…………………………………………………… 2分
即bc= b2+ c2- a2,
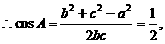 ………………………………………………4分
………………………………………………4分
∠A=60°. …………………………………………………………………………5分
(Ⅱ)∵A+B+C=180°. ∴B+C=180-60=120°.…………………………………………6分
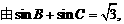
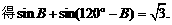 …………………………………………………………7分
…………………………………………………………7分
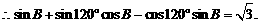 ………………………………………8分
………………………………………8分
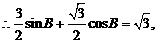
即sin(B+30°)=1. …………………………………………………………10分
∴0<B<120°,30°<B+30°<150°.
∴B+30°=90°, B=60°. ………………………………………………11分
∴A=B=C=60°,△ABC为正三角形. ………………………………………12分
14. 已知 为坐标原点,
为坐标原点, ,
,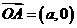 ,
,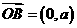 ,
,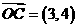 ,记
,记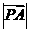 、
、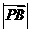 、
、 中的最大值为M,当
中的最大值为M,当 取遍一切实数时,M的取值范围是
取遍一切实数时,M的取值范围是 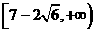 .
.
13. 函数f(x)是奇函数,且在[-1,1]是单调增函数,又f(-1)=-1, 则满足f(x)≤t2+2at+1对所有的x∈[-1,1]及a∈[-1,1]都成立的t的范围是 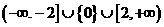 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com