
题目列表(包括答案和解析)
3. 把曲线ycosx+2y-1=0先沿x轴向右平移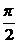 个单位,再沿y轴向下平移1个单位,得到的曲线方程是( )
个单位,再沿y轴向下平移1个单位,得到的曲线方程是( )
A.(1-y)sinx+2y-3=0 B.(y-1)sinx+2y-3=0
C.(y+1)sinx+2y+1=0 D.-(y+1)sinx+2y+1=0
2. 复数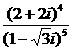 等于( )
等于( )
A.1+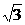 i B.-1+
i B.-1+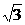 i
C.1-
i
C.1-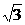 i D.-1-
i D.-1-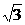 i
i
1. 定义集合运算: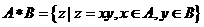 .设
.设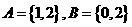 ,则集合
,则集合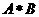 的所有元素之和为( )
的所有元素之和为( )
A.0;B.2;C.3;D.6
21.(本小题满分14分)
设数列{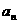 }的前n项和为
}的前n项和为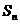 ,并且满足
,并且满足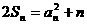 ,
,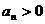 (n∈N*).
(n∈N*).
(Ⅰ)求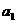 ,
, ,
,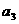 ;
;
(Ⅱ)猜想{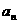 }的通项公式,并加以证明;
}的通项公式,并加以证明;
(Ⅲ)设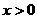 ,
,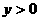 ,且
,且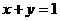 ,证明:
,证明: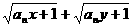 ≤
≤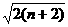 .
.
20.(本小题满分14分)
已知定圆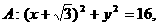 圆心为A,动圆M过点
圆心为A,动圆M过点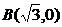 ,且和圆A相切,动圆的圆心M的轨迹记为C.
,且和圆A相切,动圆的圆心M的轨迹记为C.
(Ⅰ)求曲线C的方程;
(Ⅱ)若点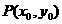 为曲线C上一点,探究直线
为曲线C上一点,探究直线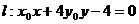 与曲线C是否存在交点? 若存在则求出交点坐标, 若不存在请说明理由.
与曲线C是否存在交点? 若存在则求出交点坐标, 若不存在请说明理由.
19.(本小题满分14分)
设函数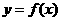 在
在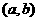 上的导函数为
上的导函数为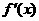 ,
,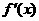 在
在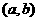 上的导函数为
上的导函数为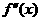 ,若在
,若在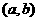 上,
上,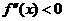 恒成立,则称函数
恒成立,则称函数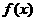 在
在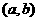 上为“凸函数”.已知
上为“凸函数”.已知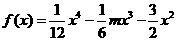 .
.
(Ⅰ)若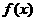 为区间
为区间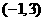 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数 的值;
的值;
(Ⅱ)若当实数 满足
满足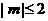 时,函数
时,函数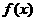 在
在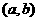 上总为“凸函数”,求
上总为“凸函数”,求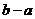 的最大值.
的最大值.
18.(本小题满分14分)
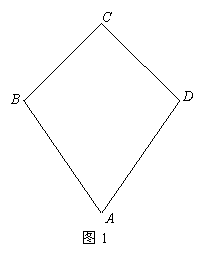
如图一,平面四边形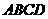 关于直线
关于直线 对称,
对称,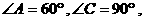
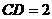 .
.
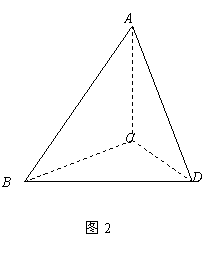 把
把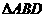 沿
沿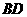 折起(如图二),使二面角
折起(如图二),使二面角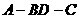 的余弦值等于
的余弦值等于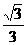 .对于图二,完成以下各小题:
.对于图二,完成以下各小题:
(Ⅰ)求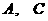 两点间的距离;
两点间的距离;
(Ⅱ)证明: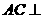 平面
平面 ;
;
 (Ⅲ)求直线
(Ⅲ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
17.(本小题满分12分)
某商场为刺激消费,拟按以下方案进行促销:顾客每消费500元便得到抽奖券一张,每张抽奖券的中奖概率为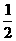 ,若中奖,商场返回顾客现金100元.某顾客现购买价格为2300的台式电脑一台,得到奖券4张.
,若中奖,商场返回顾客现金100元.某顾客现购买价格为2300的台式电脑一台,得到奖券4张.
(Ⅰ)设该顾客抽奖后中奖的抽奖券张数为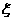 ,求
,求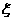 的分布列;
的分布列;
(Ⅱ)设该顾客购买台式电脑的实际支出为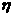 (元),用
(元),用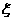 表示
表示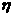 ,并求
,并求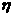 的数学期望.
的数学期望.
16. (本题满分12分)
在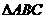 中,
中,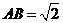 ,
,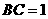 ,
,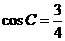 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求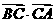 的值.
的值.
(二)选做题(13 ~ 15题,考生只能从中选做两题)
13. (不等式选讲选做题)若实数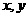 满足
满足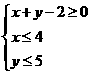 则
则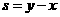 的最小值为__________.
的最小值为__________.
14. (坐标系与参数方程选做题)极坐标系中,曲线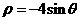 和
和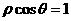 相交于点
相交于点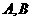 ,则
,则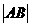 = .
= .
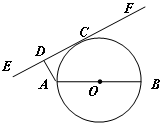
15. (几何证明选讲选做题)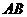 是圆
是圆 的直径,
的直径,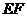 切圆
切圆 于
于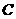 ,
,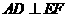 于
于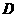 ,
,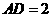 ,
,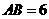 ,则
,则 的长为
.
的长为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com