
题目列表(包括答案和解析)
8.
在相距2千米的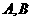 两点处测量目标C,若
两点处测量目标C,若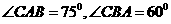 ,则
,则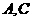 两点之间的距离是
千米.
两点之间的距离是
千米.
7.
若一个圆锥的主视图(如图所示)是边长为3,3,2的三角形,则该圆锥的侧面 积
积 为
为
6.
不等式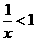 的解为
的解为
5.
若直线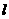 过点(3,4),且(1,2)是它的一个法向量,则直线
过点(3,4),且(1,2)是它的一个法向量,则直线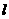 得方程为
得方程为
4.
函数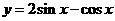 的最大值为
的最大值为
3.
若函数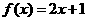 的反函数为
的反函数为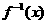 ,则
,则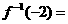
2.
计算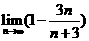 =
=
1.
 若全集
若全集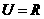 ,集合
,集合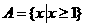 ,则
,则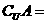
(17)(本小题满分12分)
△ABC的三个内角A,B,C所对的边分别为a,b,c,asinAsinB+bcos2A=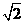 a。
a。
(I)求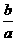 ;(II)若c2=b2+
;(II)若c2=b2+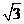 a2,求B。
a2,求B。
(18)(本小题满分12分)
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=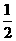 PD。
PD。
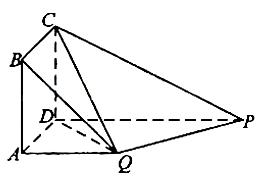
(I)证明:PQ⊥平面DCQ;
(II)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值。
19.(本小题满分12分)
某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种家和品种乙)进行田间试验。选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙。
(I)假设n=2,求第一大块地都种植品种甲的概率;
(II)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如下表:

分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
附:样本数据x1,x2,…,xa的样本方差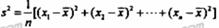 ,其中
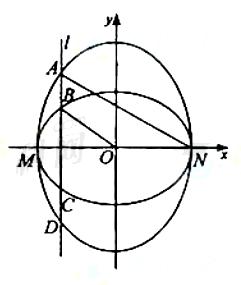
,其中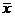 为样本平均数。
为样本平均数。
(20)(本小题满分12分)
设函数f(x)=x+ax2+blnx,曲线y=f(x)过P(1,0),且在P点处的切斜线率为2.
(I)求a,b的值;
(II)证明:f(x)≤2x-2。
(I)设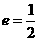 ,求
,求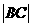 与
与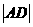 的比值;
的比值;
(II)当e变化时,是否存在直线l,使得BO∥AN,并说明理由
(21)(本小题满分12分)
如图,已知椭圆C1的中心在圆点O,长轴左、右端点M、N在x轴上,椭圆C1的短轴为MN,且C1,C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C1交于两点,这四点按纵坐标从大到小依次为A、B、C、D.
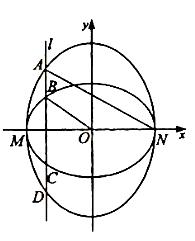
(I)设e=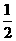 ,求|BC|与|AD|的比值;
,求|BC|与|AD|的比值;
(II)当e变化时,是否存在直线l,使得BO//AN,并说明理由.
请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题计分。做答是用2B铅笔在答题卡上把所选题目对应题号下方的方框涂黑。
(22)(本小题满分10分)选修4-1:几何证明选讲
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED。
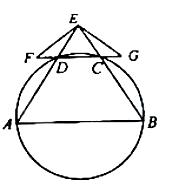
(I)证明:CD//AB;
(II)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆。
(23)(本小题满分10分)选修4-4:坐标系统与参数方程
在平面直角坐标系xOy中,曲线C1的参数方程为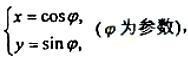 曲线C2的参数方程为
曲线C2的参数方程为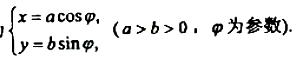 在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=a与C1,C2各有一个交点.当a=0时,这两个交点间的距离为2,当a=
在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=a与C1,C2各有一个交点.当a=0时,这两个交点间的距离为2,当a=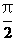 时,这两个交点重合。
时,这两个交点重合。
(I)分别说明C1,C2是什么曲线,并求出a与b的值;
(II)设当a=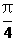 时,l与C1,C2的交点分别为A1,B1,当a=-
时,l与C1,C2的交点分别为A1,B1,当a=-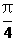 时,l与C1,
时,l与C1,
C2的交点为A2,B2,求四边形A1A2B2B1的面积。
(24)(本小题满分10分)选修4-5:不等式选讲
已知函数f(x)=|x-2|-|x-5|。
(I)证明:-3≤f(x)≤3;
(II)求不等式f(x)≥x2-8x+15的解集。
(13)已知圆C经过A(5.1),B(1.3)两点,圆心在X轴上,则C的方程为___________。
(14)调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程: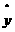 =0.254x+0.321.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加_______万元。
=0.254x+0.321.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加_______万元。
(15)Sn为等差数列{an}的前n项和,S2=S6,a4=1,则a5=____________。
(16)已知函数f(x)=ex-2x+a有另低昂,则a的取值范围是___________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com