
题目列表(包括答案和解析)
7. 一懂n层大楼,各层均可召集n个人开会,现每层指定一人到第k层开会,为使n位开会人员上下楼梯所走路程总和最短,则k应取 ( )
A.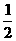 n B.
n B.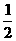 (n-1)
C.
(n-1)
C.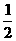 (n+1)
(n+1)
D.n为奇数时,k=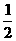 (n-1)或k=
(n-1)或k=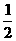 (n+1),n为偶数时k=
(n+1),n为偶数时k=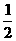 n
n
6. 数列1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,…的第1000项的值是 ( )
A. 42 B.45 C. 48 D. 51
5. 数列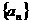 是公差不为零的等差数列,并且
是公差不为零的等差数列,并且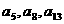 是等比数列
是等比数列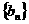 的相邻三项,若
的相邻三项,若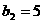 ,则
,则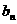 等于
( )
等于
( )
A. 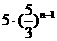 B.
B.
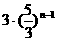
C.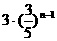 D.
D. 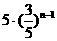
4. 已知正项等比数列数列{an},bn=log a an, 则数列{bn}是 ( )
A、等比数列 B、等差数列
C、既是等差数列又是等比数列 D、以上都不对
3. 在等差数列{a }中,3(a
}中,3(a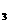 +a
+a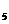 )+2(a
)+2(a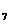 +a
+a +a
+a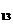 )=24,则此数列的前13项之和为 ( )
)=24,则此数列的前13项之和为 ( )
A.156 B.13
C.12 D.26
2. 已知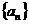 为等差数列,
为等差数列,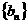 为等比数列,其公比
为等比数列,其公比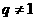 ,且
,且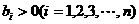 ,若
,若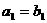 ,
,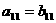 ,则
( )
,则
( )
A.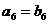 B.
B.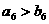
C.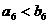 D.
D.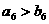 或
或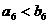
1. 已知等差数列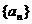 的前n项和为Sn,若
的前n项和为Sn,若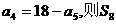 等于
( )
等于
( )
A.18 B.36
C.54 D.72
19.(本小题满分12分)已知函数f(x)=(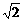 )x+a的反函数f-1(x)的图象过原点.
)x+a的反函数f-1(x)的图象过原点.
(1)若f-1(x-3),f-1(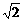 -1),f-1(x-4)成等差数列,求x的值;
-1),f-1(x-4)成等差数列,求x的值;
(2)若互不相等的三个正数m、n、t成等比数列,问f-1(m),f-1(t),f-1(n)能否组成等差数列,并证明你的结论.
考查函数与反函数概念、等差、等比的判定及综合知识能力.
[解](1)∵f-1(x)图象过(0,0),可知原函数过(0,0)
∴有(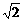 )0+a=0
)0+a=0 a=-1
a=-1
∴f(x)=(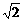 )x-1,值域{y|y>-1}
)x-1,值域{y|y>-1}
由y+1=(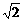 )x
)x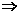 x=log
x=log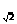 (y+1)
(y+1)
∴f-1(x)=log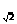 (x+1)(x>-1)
(x+1)(x>-1)
∵f-1(x-3)=log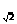 (x-2),f-1(
(x-2),f-1(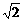 -1)=log
-1)=log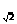
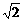 =1,
=1,
f-1(x-4)=log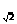 (x-3)
(x-3)
∴log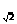 (x-2)(x-3)=(
(x-2)(x-3)=(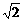 )2=2
)2=2
解得:x1=4,x2=1,
而又∵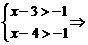 x>3,∴x=4.
x>3,∴x=4.
(2)假设f-1(m),f-1(t),f-1(n)组成等差数列,则有:
2log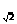 (t+1)=log
(t+1)=log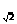 (m+1)+log
(m+1)+log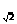 (n+1)
(n+1)
即(t+1)2=(m+1)(n+1)
化简得:2t=m+n①
又∵m、t、n成等比数列
∴t2=mn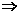 t=
t= 代入①式
代入①式
得2 =m+n即(
=m+n即( -
-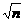 )2=0
)2=0
∴m=n,这与已知三数m、n、t互不相等矛盾.
∴f-1(m)、f-1(t)、f-1(n)不能组成等差数列.
18.(本小题满分12分)已知{an}的前n项和为Sn,且an+Sn=4.
(1)求证:数列{an}是等比数列;
(2)是否存在正整数k,使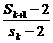 >2成立.
>2成立.
考查数列通项与前n项和关系及综合分析能力.
[解](1)由题意,Sn+an=4,Sn+1+an+1=4,
∴(Sn+1+an+1)-(Sn+an)=0
即2an+1-an=0,an+1=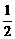 an,
an,
又2a1=S1+a1=4,∴a1=2.
∴数列{an}是以首项a1=2,公比为q=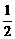 的等比数列.
的等比数列.
(2)Sn=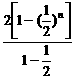 =4-22-n.
=4-22-n.
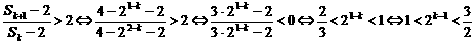
∵k∈N*,∴2k-1∈N*.
这与2k-1∈(1,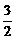 )相矛盾,故不存在这样的k,使不等式成立.
)相矛盾,故不存在这样的k,使不等式成立.
17.(本小题满分12分)设{an}为等差数列,{bn}为等比数列,a1=b1=1,a2+a4=b3,b2·b4=a3,分别求出{an}及{bn}的前10项和S10和T10.
考查等差数列、等比数列的性质及求和.
[解]∵{an}为等差数列,{bn}为等比数列.
∴a2+a4=2a3,b2·b4=b32
由已知a2+a4=b3,b2b4=a3,
∴b3=2a3,a3=b32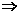 b3=2b32,
b3=2b32,
∵b3≠0,∴b3=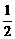 ,a3=
,a3=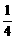 .
.
由a1=1,a3=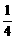
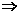 {an}公差d=-
{an}公差d=-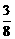 .
.
∴S10=10a1+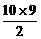 d=-
d=-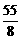
由b1=1,b3=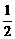 ,知{bn}公比为q=±
,知{bn}公比为q=±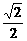 .
.
当q=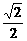 时,T10=
时,T10=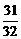 (2+
(2+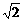 )
)
当q=-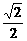 时,T10=
时,T10=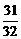 (2-
(2-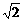 ).
).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com