
题目列表(包括答案和解析)
3.设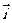 ,
,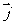 是互相垂直的单位向量,向量
是互相垂直的单位向量,向量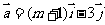 ,
,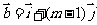 ,
,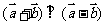 ,则实数m为
( )
,则实数m为
( )
A.-2
B.2
C.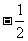 D.不存在
D.不存在
2.下列命题中,假命题为 ( )
A.
若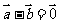 ,则
,则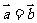 B.若
B.若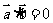 ,则
,则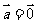 或
或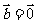
C.若k∈R,k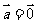 ,则k=0或
,则k=0或
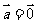
D.若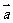 ,
,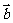 都是单位向量,则
都是单位向量,则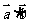 ≤1恒成立
≤1恒成立
1.
若ABCD是正方形,E是CD的中点,且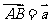 ,
,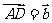 ,则
,则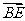 = ( )
A.
= ( )
A.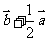 B.
B.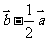 C.
C.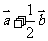 D.
D.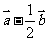
1.函数、数列、不等式应用题、排列组合问题以选择填空为主。
2概率与统计问题训练以解答题为主。
2. 某市出租车的起步价为6元,行驶路程不超过3km时,租车费为6元,若行驶路程超过3km,则按每超出1km(不足1km也按1km计程)收费3元计费.
设出租车一天行驶的路程数ξ(按整km数计算,不足1km的自动计为1km)是一个随机变量,则其收费也是一个随机变量.已知一个司机在某个月每次出车都超过了3 km,且一天的总路程数可能的取值是200、220、240、260、280、300(km),它们出现的概率依次是0.12、0.18、0.20、0.20、100a2+3a、4a.
(1)求这一个月中一天行驶路程ξ的分布列,并求ξ的数学期望和方差.
(2)求这一个月中一天所收租车费η的数学期望和方差.
解析 (1)由概率分布的性质有0.12+0.18+0.20+0.20+100a2+3a+4a=1.
∴100a2+7a=0.3,∴1 000a2+70a-3=0,a=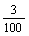 ,或a=-
,或a=-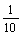 (舍去),即a=0.03,
(舍去),即a=0.03,
∴100a2+3a=0.18,4a=0.12,∴ξ的分布列为
|
ξ |
200 |
220 |
240 |
260 |
280 |
300 |
|
P |
0.12 |
0.18 |
0.20 |
0.20 |
0.18 |
0.12 |
∴Eξ=200×0.12+220×0.18+240×0.20+260×0.20+280×0.18+300×0.12=250(km)
Dξ=502×0.12+302×0.18+102×0.20+102×0.20+302×0.18+502×0.12=964;
(2)由已知η=3(ξ-3)+6=3ξ-3(ξ>3,ξ∈Z),∴Eη=E(3ξ-3)=3Eξ-3=3×250-3=747(元)
Dη=D(3ξ-3)=32Dξ=8 676.
1. 某银行准备新设一种定期存款业务,经预测,存款量与存款利率成正比,比例系数为k(k>0),贷款的利率为4.8%,假设银行吸收的存款能全部放贷出去.
(Ⅰ)若存款利率为x,x∈(0,0.048),试写出存款数量g(x)及银行应支付给储户的利息h(x)与存款利率x之间的关系式;
(Ⅱ)问存款利率为多少时,银行可获得最大收益?
解析:(Ⅰ)由题意知,存款量g(x)=kx,银行应该支付的利息h(x)=xg(x)=kx2,x∈(0,0.048).
(Ⅱ)设银行可获得收益为y,则y=0.048kx-kx2=-k(x-0.024)2+0.0242k,
当x=0.024时,y有最大值,∴存款利率定为0.024时,银行可获得最大收益.
6. 某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力,每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有60%,参加过计算机培训的有75%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(I)任选1名下岗人员,求该人参加过培训的概率;
(II)任选3名下岗人员,记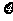 为3人中参加过培训的人数,求
为3人中参加过培训的人数,求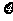 的分布列和期望.
的分布列和期望.
解:任选1名下岗人员,记“该人参加过财会培训”为事件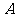 ,“该人参加过计算机培训”为事件
,“该人参加过计算机培训”为事件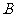 ,由题设知,事件
,由题设知,事件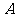 与
与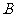 相互独立,且
相互独立,且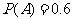 ,
,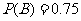 .
.
(I)解法一:任选1名下岗人员,该人没有参加过培训的概率是
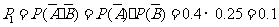
所以该人参加过培训的概率是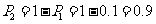 .
.
解法二:任选1名下岗人员,该人只参加过一项培训的概率是
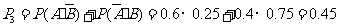
该人参加过两项培训的概率是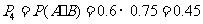 .
.
所以该人参加过培训的概率是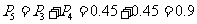 .
.
(II)因为每个人的选择是相互独立的,所以3人中参加过培训的人数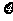 服从二项分布
服从二项分布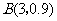 ,
,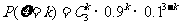 ,
,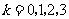 ,即
,即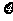 的分布列是
的分布列是
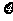 |
0 |
1 |
2 |
3 |
 |
0.001 |
0.027 |
0. 243 |
0.729 |
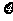 的期望是
的期望是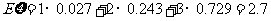 .
.
(或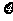 的期望是
的期望是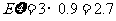 )
)
7某厂使用两种零件A、B装配两种产品P、Q,该厂的生产能力是月产P产品最多有2500件,月产Q产品最多有1200件;而且组装一件P产品要4个A、2个B,组装一件Q产品要6个A、8个B,该厂在某个月能用的A零件最多14000个;B零件最多12000个 已知P产品每件利润1000元,Q产品每件2000元,欲使月利润最大,需要组装P、Q产品各多少件?最大利润多少万元
已知P产品每件利润1000元,Q产品每件2000元,欲使月利润最大,需要组装P、Q产品各多少件?最大利润多少万元
7解 设分别生产P、Q产品x件、y件,则有
设分别生产P、Q产品x件、y件,则有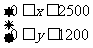 ,
,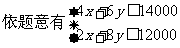 ,
,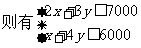 ,设利润S=1000x+2000y=1000(x+2y),要使利润S最大,只需求x+2y的最大值,
x+2y=m(2x+3y)+n(x+4y)=x(2m+n)+y(3m+4n)
,设利润S=1000x+2000y=1000(x+2y),要使利润S最大,只需求x+2y的最大值,
x+2y=m(2x+3y)+n(x+4y)=x(2m+n)+y(3m+4n)
∴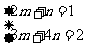 , ∴
, ∴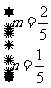 ,有x+2y=
,有x+2y=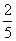 (2x+3y)+
(2x+3y)+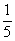 (x+4y)≤
(x+4y)≤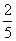 ×7000+
×7000+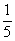 ×6000
×6000 当且仅当
当且仅当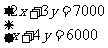 解得
解得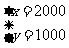 时取等号,此时最大利润Smax=1000(x+2y)=4000000=400(万元)
时取等号,此时最大利润Smax=1000(x+2y)=4000000=400(万元)
另外此题可运用“线性规划模型”解决 (万元/百台)=240(元/台)
(万元/百台)=240(元/台)
8某外商到一开放区投资72万美元建起一座蔬菜加工厂,第一年各种经费12万美元,以后每年增加4万美元,每年销售蔬菜收入50万美元
(1)若扣除投资及各种经费,则从第几年开始获取纯利润?
(2)若干年后,外商为开发新项目,有两种处理方案 ①年平均利润最大时以48万美元出售该厂;②纯利润总和最大时,以16万元出售该厂,问哪种方案最合算?
①年平均利润最大时以48万美元出售该厂;②纯利润总和最大时,以16万元出售该厂,问哪种方案最合算?
8解 由题意知,每年的经费是以12为首项,4为公差的等差数列,设纯利润与年数的关系为f(n),则f(n)=50n–[12n+
由题意知,每年的经费是以12为首项,4为公差的等差数列,设纯利润与年数的关系为f(n),则f(n)=50n–[12n+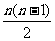 ×4]–72=–2n2+40n–72
×4]–72=–2n2+40n–72
(1)获纯利润就是要求f(n)>0,∴–2n2+40n–72>0,解得2<n<18 由n∈N知从第三年开始获利
由n∈N知从第三年开始获利
(2)①年平均利润=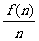 =40–2(n+
=40–2(n+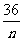 )≤16
)≤16 当且仅当n=6时取等号
当且仅当n=6时取等号 故此方案先获利6×16+48=144(万美元),此时n=6,②f(n)=–2(n–10)2+128
故此方案先获利6×16+48=144(万美元),此时n=6,②f(n)=–2(n–10)2+128
当n=10时,f(n)|max=128 故第②种方案共获利128+16=144(万美元)
故第②种方案共获利128+16=144(万美元)
故比较两种方案,获利都是144万美元,但第①种方案只需6年,而第②种方案需10年,故选择第①种方案
4 创新试题
5. 甲、乙、丙三人分别独立的进行某项技能测试,已知甲能通过测试的概率是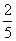 ,甲、乙、丙三人都能通过测试的概率是
,甲、乙、丙三人都能通过测试的概率是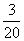 ,甲、乙、丙三人都不能通过测试的概率是
,甲、乙、丙三人都不能通过测试的概率是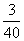 ,且乙通过测试的概率比丙大.
,且乙通过测试的概率比丙大.
(Ⅰ)求乙、丙两人各自通过测试的概率分别是多少;
(Ⅱ)求测试结束后通过的人数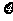 的数学期望
的数学期望 .
.
5解(Ⅰ)设乙、丙两人各自通过测试的概率分别是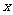 、
、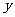 依题意得:
依题意得:

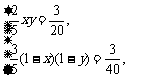 即
即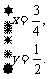 或
或 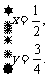 (舍去)
(舍去)
所以乙、丙两人各自通过测试的概率分别是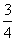 、
、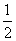 .
.
(Ⅱ)因为
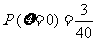 ,
,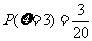 ,
,
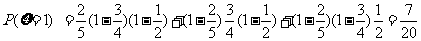
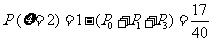 ,所以
,所以 =
=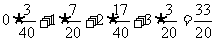 。
。
4. 已知某海滨浴场的海浪高度y(米)是时间t(0≤t≤24,单位小时)的函数,记作y=f(t),下表是某日各时的浪高数据
|
t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y(米) |
1 5 5 |
1 0 0 |
0 5 5 |
1 0 0 |
1 49 49 |
1 |
0 51 51 |
0 99 99 |
1 5 5 |
经长期观测y=f(t)的曲线可近似地看成函数y=Acosωt+b
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T,振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8 00至晚上20
00至晚上20 00之间,有多少时间可供冲浪者进行运动
00之间,有多少时间可供冲浪者进行运动
4解 (1)由表中数据,知T=12,ω=
(1)由表中数据,知T=12,ω=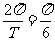
 由t=0,y=1
由t=0,y=1 5得A+b=1
5得A+b=1 5
5
由t=3,y=1 0,得b=1
0,得b=1 0
0 所以,A=0
所以,A=0 5,b=1
5,b=1 振幅A=
振幅A=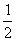 ,∴y=
,∴y=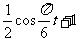
(2)由题意知,当y>1时,才可对冲浪者开放 ∴
∴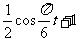 >1,
>1, 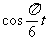 >0
>0 ∴2kπ–
∴2kπ–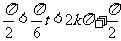 ,即有12k–3<t<13k+3
,即有12k–3<t<13k+3 由0≤t≤24,故可令k=0,1,2,得0≤t<3或9<t<15或21<t≤24
由0≤t≤24,故可令k=0,1,2,得0≤t<3或9<t<15或21<t≤24 ∴在规定时间内有6个小时可供冲浪者运动即上午9
∴在规定时间内有6个小时可供冲浪者运动即上午9 00至下午15
00至下午15 00
00
3. 我校现有教职员工500人,为了开展迎2008奥运全民健身活动,增强教职员工体质,学校工会鼓励大家积极参加晨练与晚练,每天清晨与晚上定时开放运动场、健身房和乒乓球室,约有30%的教职员工坚持每天锻炼. 据调查统计,每次去户外锻炼的人有10%下次去室内锻炼,而在室内锻炼的人有20%下次去户外锻炼. 请问,随着时间的推移,去户外锻炼的人数能否趋于稳定?稳定在多少人左右?
解:设第n次去户外锻炼的人数为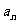 ,去室内锻炼的人为
,去室内锻炼的人为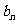 ,则有:
,则有: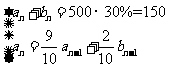 ,
,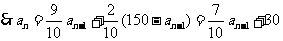 ,
,
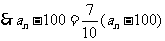 ,
,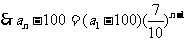 ,
,
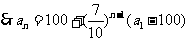
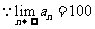 ,∴随着时间的推移,去户外锻炼的人数将稳定在100人左右 。
,∴随着时间的推移,去户外锻炼的人数将稳定在100人左右 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com