10．某市有15个旅游景点，经计算，黄金周期间各个景点的旅游人数平均为20万，标准差为s，后来经核实，发现甲、乙两处景点的旅游人数统计有误，甲景点的旅游人数实际为20万，被误统计为15万，乙景点的旅游人数实际为18万，被误统计为23万，更正后重新计算，得到的标准差为s₁，则s与s₁的大小关系为(　)

A．s＝s₁　 　　　　　 B．s＜s₁

C．s＞s₁　 　　　　　　 D．不能确定

解析：由已知得，两次统计所得的旅游人数总数没有变，即两次统计的各景点旅游人数的平均数是相同的，设为，又设各景点的实际旅游人数为x_i(1≤i≤15，i∈N^*)，则s＝

，

s₁＝

.

若比较s与s₁的大小，只需比较(15－)²+(23－)²与(20－)²+(18－)²的大小即可．而(15－)²+(23－)²＝754－76+2²，(20－)²+(18－)²＝724－76+2²，所以(15－)²+(23－)²＞(20－)²+(18－)²，从而s＞s₁.

答案：C

9．已知圆(x－4)²+y²＝a(a＞0)上恰有四个点到直线x＝－1的距离与到点(1,0)的距离相等，则实数a的取值范围为(　)

A．12＜a＜16　 　　　　　 B．12＜a＜14

C．10＜a＜16　 　　　　　 D．13＜a＜15

解析：到直线x＝－1的距离与到点(1,0)的距离相等的点的轨迹是抛物线y²＝4x，问题转化为圆与抛物线有四个交点，即联立它们的方程得到的方程组恰有四组解．

由⇒x²－4x+16－a＝0，故此方程有两个相异的正根，∴，

故12＜a＜16.

答案：A

8．已知双曲线过点(4，)，渐近线方程为y＝±x，圆C经过双曲线的一个顶点和一个焦点且圆心在双曲线上，则圆心到该双曲线的中心的距离是(　)

A.　 B.　 C．4　 D.

解析：由题意易得双曲线的方程为－＝1，顶点为(±3,0)，焦点为(±5,0)．又圆心在双曲线上，所以圆C应过左顶点、左焦点或右顶点、右焦点，即圆心的横坐标为±4，设圆心的纵坐标为m，则－＝1，所以m²＝＝，所求的距离为 ＝.

答案：D

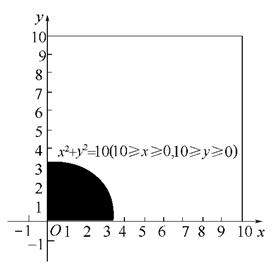
7．在区间[0,10]内随机取出两个数，则这两个数的平方和也在区间[0,10]内的概率是(　)

A.　 B.　 C.　 D.

解析：将取出的两个数分别用x，y表示，则0≤x≤10,0≤y≤10.如图，当点(x，y)落在图中的阴影区域时，取出的两个数的平方和也在区间[0,10]内，故所求概率为＝.

答案：D

6．若i是虚数单位，z＝2－i+ai²⁰⁰⁹(a∈R)是实数，则()²⁰⁰⁹等于(　)

A．2　 B．2i　 C．i　 D．2²⁰⁰⁹

解析：∵z＝2－i+ai²⁰⁰⁹＝2+(a－1)i为实数，∴a－1＝0，即a＝1，∴()²⁰⁰⁹＝()²⁰⁰⁹＝i²⁰⁰⁹＝i.

答案：C

5．已知回归直线斜率的估计值为1.23，样本点的中心为点(4,5)，则回归直线的方程为(　)

A.＝1.23x+4　 　　　　　　　　 B.＝1.23x+5

C.＝1.23x+0.08　 　　　　　　 D.＝0.08x+1.23

解析：回归直线必过点(4,5)，故其方程为－5＝1.23(x－4)，即＝1.23x+0.08.

答案：C

4．已知a，b表示两条不同的直线，α，β，γ表示三个不同的平面，有下列四个命题：

①若α∩β＝a，β∩γ＝b，且a∥b，则α∥γ；

②若a，b相交，且都在α、β外，a∥α，a∥β，b∥α，b∥β，则α∥β；

③若α⊥β，α∩β＝a，b⊂β，a⊥b，则b⊥α；

④若a⊂α，b⊂α，l⊥a，l⊥b，则l⊥α.

其中正确命题的序号是(　)

A．①②　 B．②③　 C．③④　 D．①④

解析：①错误，因为三个平面可以两两相交且交线相互平行；④错误，因为只有a，b相交时结论才成立．

答案：B

3．过曲线y＝x³－2x+4上的点(1,3)作两条互相垂直的直线l₁，l₂，若直线l₁是曲线y＝x³－2x+4的切线，则直线l₂的倾斜角为(　)

A.　　B.　　C.　　D.

解析：∵y＝x³－2x+4，∴y′＝3x²－2，

∴直线l₁的斜率为y′|_x＝1＝1，

又l₁⊥l₂，∴直线l₂的斜率为－1，

∴直线l₂的倾斜角为.

答案：D

2．已知a，b是两个不共线的向量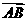，＝λa+b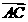，＝a+μb(λ，μ∈R)，那么A、B、C三点共线的充要条件是(　)

A．λ+μ＝2　 B．λ－μ＝1

C．λμ＝－1　 D．λμ＝1

解析：由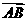＝λa+b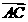，＝a+μb(λ，μ∈R)及A、B、C三点共线得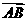：＝t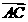 (t∈R)，所以λa+b＝t(a+μb)＝ta+tμb，所以，所以λμ＝1.

答案：D

1．若集合A＝{x|＞2，x∈R}，非空集合B满足(A∪B)⊆(A∩B)，则有∁_RB＝(　)

A．(0，)　　　 　　　　 B．(－∞，0]∪[，+∞)

C．(－∞，)　 　　　　　　　　　　　　　 D．[，+∞)

解析：由(A∪B)⊆(A∩B)得A∪B＝A∩B，所以A＝B，即B＝{x|＞2，x∈R}＝{x|0＜x＜}，故∁_RB＝(－∞，0]∪[，+∞)．

答案：B