
题目列表(包括答案和解析)
3.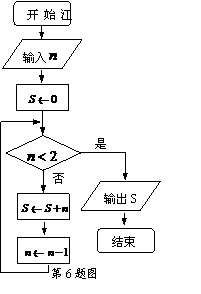 已知集合
已知集合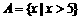 ,集合
,集合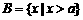 ,若命题
,若命题
“ ”是命题“
”是命题“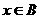 ”的充分不必要条件,则实
”的充分不必要条件,则实
数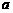 的取值范围是 .
的取值范围是 .
2. 某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20 种,从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是 .
1. 复数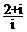 在复平面上对应的点在第 象限.
在复平面上对应的点在第 象限.
23.[必做题]本题满分10分.解答时应写出文字说明、证明过程或演算步骤.
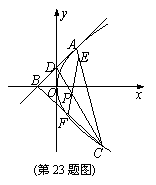 过抛物线y2=4x上一点A(1,2)作抛物线的切线,分别交x轴于点B,交y轴于点D,点C(异于点A)在抛物线上,点E在线段AC上,满足
过抛物线y2=4x上一点A(1,2)作抛物线的切线,分别交x轴于点B,交y轴于点D,点C(异于点A)在抛物线上,点E在线段AC上,满足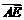 =λ1
=λ1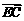 ;点F在线段BC上,满足
;点F在线段BC上,满足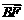 =λ2
=λ2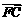 ,且λ1+λ2=1,线段CD与EF交于点P.
,且λ1+λ2=1,线段CD与EF交于点P.
(1)设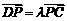 ,求
,求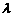 ;
;
(2)当点C在抛物线上移动时,求点P的轨迹方程.
解:(1)过点A的切线方程为y=x+1. …………………………………………………1分
切线交x轴于点B(-1,0),交y轴交于点D(0,1),则D是AB的中点.
所以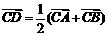 .
(1) ………………………3分
.
(1) ………………………3分
由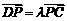 Þ
Þ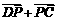 =(1+λ)
=(1+λ)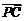 Þ
Þ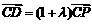 . (2)
. (2)
同理由 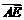 =λ1
=λ1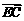 , 得
, 得 =(1+λ1)
=(1+λ1)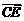 , (3)
, (3)
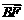 =λ2
=λ2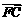 , 得
, 得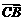 =(1+λ2)
=(1+λ2)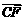 . (4)
. (4)
将(2)、(3)、(4)式代入(1)得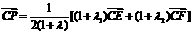 .
.
因为E、P、F三点共线,所以 + =1,
再由λ1+λ2=1,解之得λ=.……………………………………………………………6分
(2)由(1)得CP=2PD,D是AB的中点,所以点P为△ABC的重心.
所以,x=,y=.
解得x0=3x,y0=3y-2,代入y02=4x0得,(3y-2)2=12x.
由于x0≠1,故x≠3.所求轨迹方程为(3y-2)2=12x (x≠3). ………………………10分
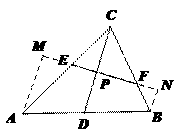
本题以抛物线为载体,巧妙整合平面几何中如下一个著名结论命制而成的。
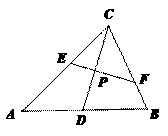 如图,
如图,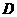 是
是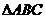 的中点,
的中点,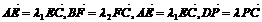 ,
,
则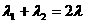 .
.
证明1 设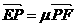 ,则
,则
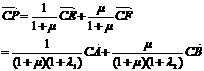 ,
,
又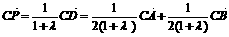 ,
,
∴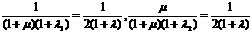 ,
,
则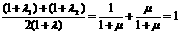
证明2 作如图所示的辅助线,其中 ∥
∥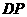 ∥
∥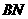 ,
,
则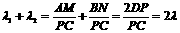
说明:根据上题结论不难得知,本题第1小问结果为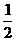 ;
;
(2)第2小问利用点转移法即可求得点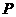 的轨迹方程.标答中用了三角形的重心公式,事实上无此必要,设
的轨迹方程.标答中用了三角形的重心公式,事实上无此必要,设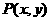 ,由
,由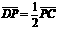 即可得点
即可得点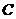 坐标,而
坐标,而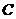 在抛物线上运动,下同标答.
在抛物线上运动,下同标答.
把握了命题人的思维脉搏,我们知道了本题的由来,如果将抛物线换成其他曲线,也可得一些类似的问题。
23.考查曲线的轨迹方程的探求及综合应用能力.
22.[必做题]本题满分10分.解答时应写出文字说明、证明过程或演算步骤.
已知函数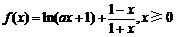 ,其中a>0.
,其中a>0.
(1)若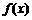 在x=1处取得极值,求a的值;
在x=1处取得极值,求a的值;
(2)若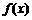 的最小值为1,求a的取值范围.
的最小值为1,求a的取值范围.
解:(1)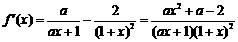 .
.
因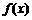 在
在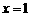 处取得极值,故
处取得极值,故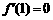 ,解得a=1 (经检验).……………………4分
,解得a=1 (经检验).……………………4分
(2)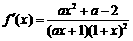 ,因
,因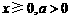 ,故ax+1>0,1+x>0.
,故ax+1>0,1+x>0.
当a≥2时,在区间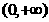 上
上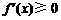 ,
,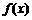 递增,
递增,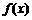 的最小值为f(0)=1.
的最小值为f(0)=1.
当0<a<2时,由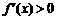 ,解得
,解得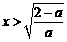 ;由
;由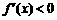 ,解得
,解得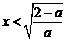 .
.
∴f(x)的单调减区间为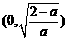 ,单调增区间为
,单调增区间为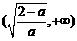 .
.
于是,f(x)在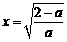 处取得最小值
处取得最小值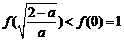 ,不合.
,不合.
综上可知,若f(x)得最小值为1,则a的取值范围是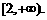 ……………………10分
……………………10分
注:不检验不扣分.
22.考查复合函数求导的基础知识以及导数知识的综合应用.
21. [选做题]本题包括A,B,C,D共4小题,请从这4题中选做2小题,每小题10分,共20分.请在答题卡上准确填涂题目标记,解答时应写出文字说明、证明过程或演算步骤.
[选做题]本题包括A,B,C,D共4小题,请从这4题中选做2小题,每小题10分,共20分.请在答题卡上准确填涂题目标记,解答时应写出文字说明、证明过程或演算步骤.
A.选修4-1:几何证明选讲
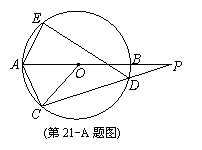
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,求证:∠PDE=∠POC.
证明:因AE=AC,AB为直径,
故∠OAC=∠OAE. ……………………………………………………………3分
所以∠POC=∠OAC+∠OCA=∠OAC+∠OAC=∠EAC.
又∠EAC=∠PDE,
所以,∠PDE=∠POC.…………………………………………………………10分
B.选修4-2:矩阵与变换
已知圆C: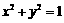 在矩阵
在矩阵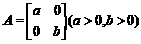 对应的变换作用下变为椭圆
对应的变换作用下变为椭圆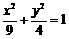 ,求a,b的值.
,求a,b的值.
解:设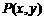 为圆C上的任意一点,在矩阵A对应的变换下变为另一个点
为圆C上的任意一点,在矩阵A对应的变换下变为另一个点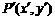 ,
,
则 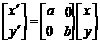 ,即
,即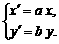 …………………………………………………4分
…………………………………………………4分
又因为点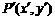 在椭圆
在椭圆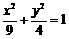 上,所以
上,所以 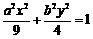 .
.
由已知条件可知,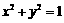 ,所以 a2=9,b2=4.
,所以 a2=9,b2=4.
因为 a>0 ,b>0,所以 a=3,b=2. …………………………………………………10分
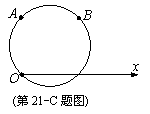 C.选修4-4:坐标系与参数方程
C.选修4-4:坐标系与参数方程
在极坐标系中,求经过三点O(0,0),A(2,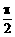 ),B(
),B(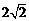 ,
,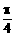 )
)
的圆的极坐标方程.
解:设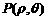 是所求圆上的任意一点,………………………………………………3分
是所求圆上的任意一点,………………………………………………3分
则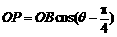 ,
,
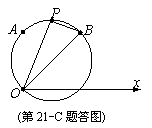 故所求的圆的极坐标方程为
故所求的圆的极坐标方程为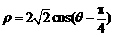 . …………………………………10分
. …………………………………10分
注: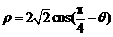 亦正确.
亦正确.
D.选修4-5:不等式选讲
已知x,y,z均为正数.求证: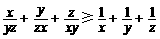 .
.
证明:因为x,y,z都是为正数,所以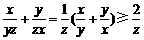 .
…………………3分
.
…………………3分
同理可得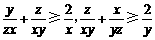 .
.
将上述三个不等式两边分别相加,并除以2,得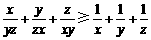 .………10分
.………10分
20.(本题满分16分)
综合考查函数与导数的基础知识与基本内容,考查分类讨论的意识以及独立分析问题与解决问题的能力.
设函数f(x)=ax3-(a+b)x2+bx+c,其中a>0,b,c∈R.
(1)若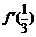 =0,求函数f(x)的单调增区间;
=0,求函数f(x)的单调增区间;
(2)求证:当0≤x≤1时,|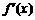 |≤
|≤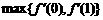 .(注:max{a,b}表示a,b中的最大值)
.(注:max{a,b}表示a,b中的最大值)
解:(1)由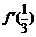 =0,得a=b.
…………………………………………………………1分
=0,得a=b.
…………………………………………………………1分
故f(x)= ax3-2ax2+ax+c.
由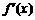 =a(3x2-4x+1)=0,得x1=
=a(3x2-4x+1)=0,得x1=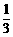 ,x2=1.…………………………………………2分
,x2=1.…………………………………………2分
列表:
|
x |
(-∞,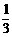 ) ) |
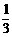 |
(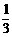 ,1) ,1) |
1 |
(1,+∞) |
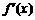 |
+ |
0 |
- |
0 |
+ |
|
f(x) |
增 |
极大值 |
减 |
极小值 |
增 |
由表可得,函数f(x)的单调增区间是(-∞,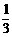 )及(1,+∞) .…………………………4分
)及(1,+∞) .…………………………4分
(2)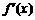 =3ax2-2(a+b)x+b=3
=3ax2-2(a+b)x+b=3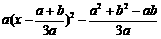 .
.
①当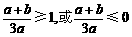 时,则
时,则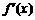 在
在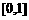 上是单调函数,
上是单调函数,
所以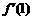 ≤
≤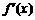 ≤
≤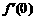 ,或
,或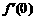 ≤
≤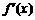 ≤
≤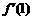 ,且
,且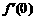 +
+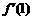 =a>0.
=a>0.
所以|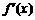 |≤
|≤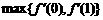 .………………………………………………………8分
.………………………………………………………8分
②当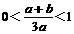 ,即-a<b<2a,则
,即-a<b<2a,则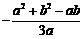 ≤
≤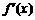 ≤
≤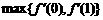 .
.
(i) 当-a<b≤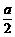 时,则0<a+b≤
时,则0<a+b≤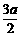 .
.
所以 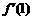
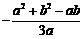 =
=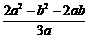 =
=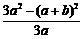 ≥
≥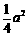 >0.
>0.
所以 |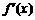 |≤
|≤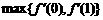 . ……………………………………………………12分
. ……………………………………………………12分
(ii) 当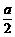 <b<2a时,则
<b<2a时,则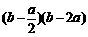 <0,即a2+b2-
<0,即a2+b2-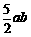 <0.
<0.
所以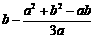 =
=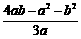 >
>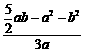 >0,即
>0,即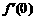 >
>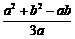 .
.
所以 |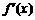 |≤
|≤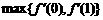 .
.
综上所述:当0≤x≤1时,|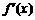 |≤
|≤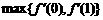 .……………………………16分
.……………………………16分
数学Ⅱ(附加题)
19.(本题满分16分)
已知数列{an}满足:a1=a2=a3=2,an+1=a1a2…an-1(n≥3),记
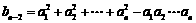 (n≥3).
(n≥3).
(1)求证数列{bn}为等差数列,并求其通项公式;
(2)设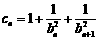 ,数列{
,数列{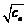 }的前n项和为Sn,求证:n<Sn<n+1.
}的前n项和为Sn,求证:n<Sn<n+1.
解:(1)方法一 当n≥3时,因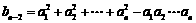 ①,
①,
故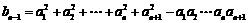 ②. ……………………………………2分
②. ……………………………………2分
②-①,得 bn-1-bn-2=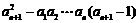 =
=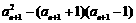 =1,为常数,
=1,为常数,
所以,数列{bn}为等差数列. …………………………………………………………5分
因 b1=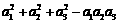 =4,故 bn=n+3. ……………………………………8分
=4,故 bn=n+3. ……………………………………8分
方法二 当n≥3时,a1a2…an=1+an+1,a1a2…anan+1=1+an+2,
将上两式相除并变形,得 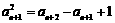 .……………………………………2分
.……………………………………2分
于是,当n∈N*时,
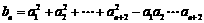
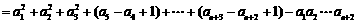
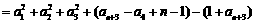
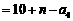 .
.
又a4=a1a2a3-1=7,故bn=n+3(n∈N*).
所以数列{bn}为等差数列,且bn=n+3. ………………………………………………8分
(2) 方法一 因 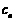
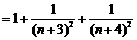
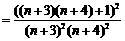 ,…………………12分
,…………………12分
故 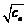
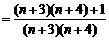
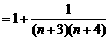
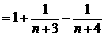 .
.
所以 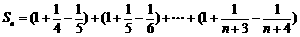
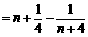 , ………15分
, ………15分
即 n<Sn<n+1. ………………………………………………………………………16分
方法二 因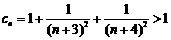 ,故
,故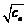 >1,
>1,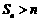 .……………………10分
.……………………10分
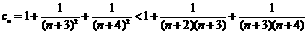
=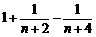 <
<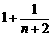 <
<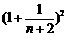 ,
,
故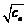 <
<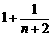 ,于是
,于是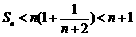 .……………………………………16分
.……………………………………16分
第(2)问,为了结果的美观,将Sn放缩范围放得较宽,并且可以改为求不小于Sn的最小正整数或求不大于Sn的最大正整数.
本题(2)的方法二是错误的,请不要采用。
注意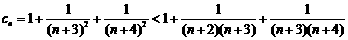
=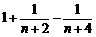 <
<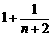 <
<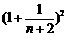 ,
,
故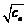 <
<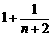 ,于是
,于是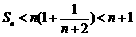 .
.
于是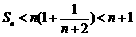 。(这一步推理是错误的)
。(这一步推理是错误的)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com