
题目列表(包括答案和解析)
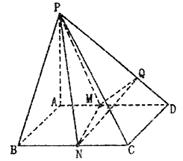
17.(本小题满分12分)已知四棱锥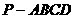 (如图)底面是边长为2的正方形.
(如图)底面是边长为2的正方形.
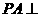 平面
平面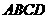 ,
,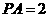 ,
,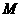 ,
,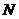 分别为
分别为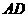 ,
,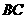 的中点,
的中点,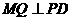 于
于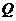 .
.
 (Ⅰ)求证:平面
(Ⅰ)求证:平面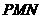 ⊥平面
⊥平面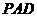 ;
;
(Ⅱ)求二面角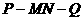 的余弦值.
的余弦值.
16.(本小题满分12分)在锐角△ABC中,a, b, c分别为内角A, B, C的对边,且

(Ⅰ)求A的大小;
(Ⅱ)求表达式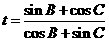 的取值范围.
的取值范围.
15.(在给出的二个题中,任选一题作答. 若多选做,则
按所做的第一题给分)
(1)(坐标系与参数方程)在极坐标系中,曲线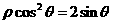 的焦点的极坐标为
.
的焦点的极坐标为
.
(2)(不等式选讲)若不等式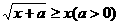 的解集为
的解集为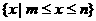 ,且
,且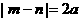 ,则a的取值集合为
.
,则a的取值集合为
.
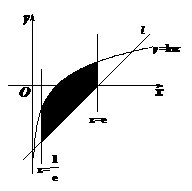
14. 由函数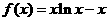 的图像在点
的图像在点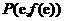 处的切
处的切
线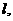 直线
直线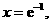 直线
直线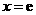 (其中
(其中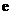 是自然对数的底
是自然对数的底
数)及曲线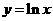 所围成的曲边四边形(如图中的阴
所围成的曲边四边形(如图中的阴
影部分)的面积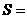 .
.
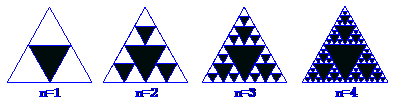
13. 图中的三角形称为谢宾斯基(Sierpinski)三角形。在下图中,将第1个三角形的三边中点为顶点的三角形着色,将第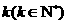 个图形中的每个未着色三角形的三边中点为顶点的三角形着色,得到第
个图形中的每个未着色三角形的三边中点为顶点的三角形着色,得到第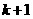 个图形, 这样这些图形中着色三角形的个数依次构成一个数列
个图形, 这样这些图形中着色三角形的个数依次构成一个数列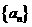 ,则数列
,则数列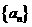 的通项公式为
.
的通项公式为
.


12. 设圆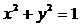 的切线与
的切线与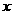 轴的正半轴,
轴的正半轴,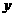 轴的正半轴分别交于点
轴的正半轴分别交于点 ,
,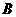 ,当
,当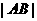 取最小值时,切线的方程为
.
取最小值时,切线的方程为
.
11.某校为了解高三同学寒假期间学习情况,调查了100名
同学,统计他们每天平均学习时间,绘成频率分布直方
图(如图).则这100名同学中学习时间在6至8小时
的同学为 人.
10.已知定义域为区间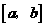 的函数
的函数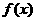 ,其图象是一条连续不断地曲线,且满足下列条件:①
,其图象是一条连续不断地曲线,且满足下列条件:①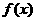 的值域为
的值域为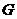 ,且
,且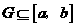 ;②对任意不同的
;②对任意不同的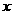 、
、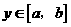 ,都有
,都有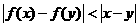 ,那么函数
,那么函数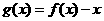 在区间[
在区间[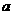 ,
, ]上( )
]上( )
A.没有零点 B. 有且只有一个零点
C.恰有两个不同的零点 D.有无数个不同的零点
第Ⅱ卷
9.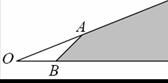 已知数列
已知数列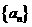 满足
满足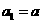 ,且
,且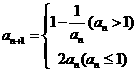 ,对任意的
,对任意的
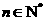 ,总有
,总有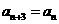 成立,则
成立,则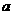 在
在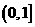 内的可能值有( )
内的可能值有( )
A.1个 B.2个 C.3个 D.4个
8. 如下图所示,两射线 与
与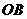 交于点
交于点 ,下列5个向量中,
,下列5个向量中,
①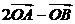 ②
②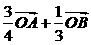 ③
③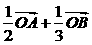
④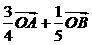 ⑤
⑤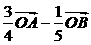
若以 为起点,终点落在阴影区域内(含边界)的向量有( )个.
为起点,终点落在阴影区域内(含边界)的向量有( )个.
A.1 B. 2 C. 3 D.4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com